
Kenarortay Formülleri Nelerdir?
Kenarortay, bir üçgenin köşelerinden birinden karşı kenarına çizilen ve o kenarı iki eşit parçaya bölen doğru parçasıdır. Bu kavram, üçgenlerin geometrik özelliklerini anlamak ve hesaplamak için kritik bir öneme sahiptir. Kenarortay formülleri, mühendislik ve mimarlık gibi alanlarda uygulama bulur.
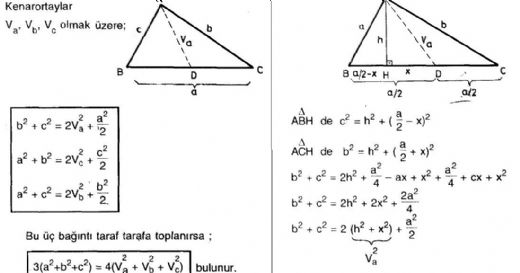
Kenarortay, geometri alanında önemli bir kavramdır ve genellikle üçgenler üzerinde çalışılırken karşımıza çıkar. Kenarortay, bir üçgenin bir köşesinden karşı kenarına kadar olan doğru parçasıdır ve karşı kenarı iki eşit parçaya böler. Bu yazıda, kenarortay formülleri, özellikleri ve uygulamaları hakkında detaylı bir inceleme sunulacaktır. Kenarortay Nedir?Kenarortay, bir üçgenin köşelerinden birinden karşı kenarına çizilen ve o kenarı iki eşit parçaya bölen doğru parçasıdır. Her üçgenin üç adet kenarortayı bulunur ve bu kenarortaylar üçgenin ağırlık merkezi ile kesişir. Üçgenin ağırlık merkezi, kenarortayların kesişim noktasıdır ve genellikle "G" harfi ile gösterilir. Kenarortay Formülü Bir üçgenin kenarortayını hesaplamak için kullanılan temel formül, kenarortayın uzunluğunu belirlemeye yarar. Aşağıda, bir üçgenin kenarortayını bulmak için kullanılan formül verilmiştir:
Kenarortayların Özellikleri Kenarortayların bazı önemli özellikleri şunlardır:
Kenarortayların Uygulamaları Kenarortaylar, geometri derslerinde olduğu kadar mühendislik ve mimarlık alanlarında da önemli bir yer tutar. Kenarortayların bazı uygulamaları şunlardır:
Sonuç Kenarortaylar, üçgenlerin geometrik özelliklerini anlamak ve hesaplamak için temel unsurlardan biridir. Kenarortay formülü, üçgenin kenarları arasındaki ilişkiyi belirlemekte ve çeşitli alanlarda uygulama imkanı sunmaktadır. Geometri derslerinden mühendislik uygulamalarına kadar geniş bir yelpazede önemli bir yere sahiptir. Ekstra Bilgiler Kenarortayların daha karmaşık geometrik yapıların analizinde de kullanıldığı bilinmektedir. Örneğin, çokgenlerin kenarortayları, çokgenin simetrik özelliklerini incelemek için kullanılabilir. Ayrıca, bilgisayar grafikleri ve modelleme alanlarında, kenarortaylar, nesnelerin düzgün ve estetik şekillerde tasarlanmasında önemli bir rol oynar. |















































Kenarortay formülleri hakkında okuduklarım gerçekten ilginç. Eski medeniyetlerin bu formülleri kullanarak geometrik ilişkileri tanımlamış olmaları, matematiğin tarihsel gelişimi açısından oldukça etkileyici. Kenarortaylar ile ilgili özelliklerin yanı sıra, eşkenar üçgenlerde açıortay ve kenarortayın birbirine eşit olması da dikkat çekici bir durum. Üçgenlerin iç açıları toplamının her zaman 180 derece olması, geometri derslerinde en temel bilgilerden biri. Kenarortay formüllerinin, üçgenlerin kenarları ve açıları arasındaki ilişkileri anlamada önemli bir rol oynaması, matematiksel düşüncenin temellerini oluşturuyor. Özellikle dik üçgende kenarortay uzunluğunun hipotenüsün yarısına eşit olması gibi pratik bilgiler, geometri uygulamalarında sıkça karşılaştığımız durumlar. Bu formüllerin günlük hayatta da nasıl uygulanabileceğini merak ediyorum. Sizce bu formüller dışında başka hangi geometrik özellikler günlük yaşamda karşımıza çıkıyor?
Nebihe Hanım,
Yorumunuzda kenarortay formüllerinin tarihsel önemi ve geometrik ilişkilerdeki rolü üzerine oldukça güzel bir değerlendirme yapmışsınız. Matematiğin Tarihsel Gelişimi açısından eski medeniyetlerin bu formülleri kullanması, matematiksel düşüncenin evrimi hakkında önemli bilgiler sunuyor. Özellikle, Üçgenlerin İç Açıları toplamının her zaman 180 derece olması gibi temel bilgiler, geometri derslerinde öğrencilere kazandırılan en önemli kavramlar arasında yer alıyor.
Günlük yaşamda, Geometrik Özelliklerin Uygulanması konusunda birçok örnekle karşılaşabiliriz. Örneğin, mimaride ve inşaatta kullanılan açılar ve kenar uzunlukları, projelerin sağlamlığını ve estetiğini belirler. Ayrıca, Üçgenlerin Kullanımı yapıların dayanıklılığında önemli bir yere sahiptir; çünkü üçgenler, en sağlam geometrik şekillerden biri olarak bilinir.
Bunun yanı sıra, Günlük Hayatta Geometrik Hesaplamalar yaparken, alan ve hacim hesapları, mobilya yerleşim planları veya bahçe düzenlemeleri gibi konularda sıkça kullanılır. Kenarortaylar ve açıortaylar gibi kavramlar, bu durumlarda pratik ve işlevsel bir şekilde karşımıza çıkar.
Sonuç olarak, geometri ve onun temel ilkeleri günlük yaşamımızda pek çok alanda karşımıza çıkmakta ve hayatımızı kolaylaştıran araçlar sağlamaktadır. Geometrik düşünmenin bu kadar geniş bir yelpazeye yayılması, matematiğin sadece soyut bir disiplin olmadığını, aynı zamanda pratik bir uygulama alanı sunduğunu gösteriyor.
Saygılarımla,