Kürenin Hacim Formülü Nelerdir?
Kürenin hacim formülü, üç boyutlu geometrik nesnelerin hacim hesaplamalarında kritik bir öneme sahiptir. Bu makalede, kürenin hacminin nasıl hesaplandığı, formülün türetilmesi ve çeşitli uygulama alanları detaylandırılmaktadır. Matematiksel ve fiziksel açıdan sağladığı katkılar ele alınacaktır.
Küresel geometrik şekiller, matematiksel ve fiziksel uygulamalarda önemli bir yere sahiptir. Küre, üç boyutlu bir nesne olarak, her noktası merkezine eşit uzaklıkta bulunan bir yüzeydir. Bu makalede, kürenin hacim formülü, türetilmesi ve uygulamaları üzerinde durulacaktır. Kürenin Hacmi Nedir?Kürenin hacmi, bir küre içerisinde yer alan alanın ölçüsüdür. Matematiksel olarak, bir kürenin hacmi, yer kaplayan madde miktarını ifade eder ve genellikle \( V \) harfi ile gösterilir. Hacim, belirli bir formül kullanılarak hesaplanabilir. Kürenin Hacim Formülü Kürenin hacmi, aşağıdaki formül ile hesaplanır:\[ V = \frac{4}{3} \pi r^3 \]Burada;- \( V \): Kürenin hacmi- \( r \): Kürenin yarıçapı- \( \pi \): Yaklaşık değeri 3.14159 olan matematiksel bir sabittir. Hacim Hesaplaması Bir kürenin hacmini hesaplamak için önce yarıçapın belirlenmesi gerekmektedir. Yarıçap, kürenin merkezinden yüzeyine olan mesafedir. Örneğin, bir kürenin yarıçapı 5 cm ise, hacim şu şekilde hesaplanır:\[ V = \frac{4}{3} \pi (5)^3 = \frac{4}{3} \pi (125) \approx 523.6 \, \text{cm}^3 \] Kürenin Hacim Formülünün Türetimi Kürenin hacim formülünün türetilmesi, integral hesaplamaları kullanılarak yapılır. Bir küre, sonsuz sayıda ince dairesel dilimlerden oluştuğu düşünülerek, bu dilimlerin hacimlerinin toplamı alınır.1. Dairesel Kesitlerin Alanı: Kürenin merkezinde bulunan bir kesit, bir daire oluşturur. Bu dairenin alanı \( A = \pi r^2 \) formülü ile hesaplanır. 2. Dilimlerin Hacmi: Bu dairesel dilimlerin yüksekliği, \( dh \) olarak kabul edilirse, her dilimin hacmi \( dV = A \cdot dh = \pi r^2 \cdot dh \) şeklindedir. 3. Toplam Hacim: Kürenin tüm dilimlerinin hacmini toplamak için uygun integral sınırları belirlenir ve integral alınır. Sonuçta, yukarıda belirtilen formül elde edilir. Kürenin Hacim Formülünün Uygulamaları Kürenin hacim formülü, çeşitli alanlarda birçok uygulama bulmaktadır:
Sonuç Kürenin hacim formülü, matematiksel ve fiziksel uygulamalarda önemli bir yere sahiptir. Bu formül, küresel nesnelerin hacimlerini hesaplamak için basit ve etkili bir yöntem sunmaktadır. Kürelerin hacim hesaplamaları, mühendislikten fiziğe kadar geniş bir yelpazede kullanılmakta ve araştırmalara yön vermektedir. Matematiksel olarak türetilmesi, analitik düşünmeyi teşvik eder ve bu tür hesaplamaların temelini anlamaya yardımcı olur. |
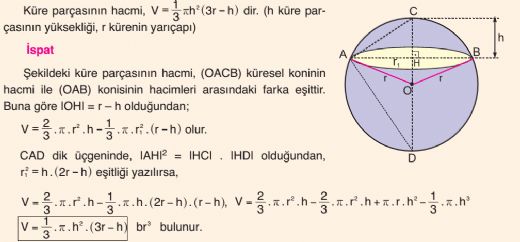



































Kürede hacim hesaplamak çok keyifli! Yarım kürenin hacmi formülü, kısmen daha basit. Yarım kürenin hacmi, V = (2/3)πr³ ile hesaplanır. Bu formül sayesinde, yarım kürelerin hacimlerini kolayca bulmak mümkün. Matematiksel uygulamalardaki önemi ise tartışılmaz!
Merhaba GÜROL,
Yorumunuzda yarım kürenin hacim formülünü ve matematiksel uygulamalardaki önemini vurguladığınız için teşekkür ederim. Gerçekten de hacim hesaplama, geometrinin temel konularından biri ve yarım küreler gibi özel şekillerin incelenmesi, birçok alanda pratik uygulamalara dönüşebiliyor. Özellikle mühendislik ve mimarlıkta bu tür hesaplamaların önemi büyük. Ayrıca, matematiksel kavramların günlük yaşamda nasıl kullanıldığını görmek oldukça keyifli. Hacim hesaplama sayesinde, çeşitli tasarımların ve yapılarının ne kadar malzeme gerektireceğini hesaplayabiliyoruz. Bu da hem maliyet hem de kaynak yönetimi açısından oldukça faydalı. Matematiğe olan bu ilginiz devam etsin!
Saygılarımla.
Küresel geometrik şekiller arasında yarım küre, hacim hesaplamaları açısından oldukça ilginçtir. Yarım kürenin hacmi, tam kürenin hacminin yarısı olarak hesaplanabilir. Peki, yarım kürenin hacmi nasıl bulunur? Bunun için hacim formülü kullanarak örnekler verebilir misiniz?
Yarım Kürenin Hacmi Hesaplama
Rabi, yarım kürenin hacmini hesaplamak için öncelikle tam kürenin hacim formülünü bilmek gerekir. Tam bir kürenin hacmi, aşağıdaki formül ile hesaplanır:
\[ V = \frac{4}{3} \pi r^3 \]
Burada \( V \) hacmi, \( r \) ise kürenin yarıçapını temsil etmektedir. Yarım kürenin hacmi ise tam kürenin hacminin yarısı olduğu için şu şekilde hesaplanır:
\[ V_{yarım\ küre} = \frac{1}{2} \times \frac{4}{3} \pi r^3 = \frac{2}{3} \pi r^3 \]
Örnek Hesaplamalar
Örnek vermek gerekirse, eğer yarım kürenin yarıçapı \( r = 3 \) cm ise, yarım kürenin hacmi şöyle hesaplanır:
\[ V_{yarım\ küre} = \frac{2}{3} \pi (3)^3 = \frac{2}{3} \pi \times 27 = 18\pi \]
Bu durumda yarım kürenin hacmi yaklaşık olarak 56.55 cm³ olacaktır (π ≈ 3.14 alındığında).
Bir başka örnekte, yarım kürenin yarıçapı \( r = 5 \) cm olsun:
\[ V_{yarım\ küre} = \frac{2}{3} \pi (5)^3 = \frac{2}{3} \pi \times 125 = \frac{250}{3}\pi \]
Bu durumda yarım kürenin hacmi yaklaşık olarak 261.80 cm³ olacaktır.
Yarım küre hacmi hesaplaması, özellikle mühendislik ve mimarlık gibi alanlarda oldukça önemli bir yer tutar. Bu bilgiler ışığında yarım küre hacmi hesaplamalarının ne kadar pratik ve faydalı olduğunu görebiliriz.
Kürede hacmi hesaplamak oldukça ilginç. Yarıçapı kullanarak formülü uygulamak, kürenin hacmini belirlemede temel bir adım. Kürenin hacmi nasıl hesaplanır sorusunu sormak, anlamayı kolaylaştırıyor. Kürenin hacmini bulduktan sonra, diğer geometrik şekillerle karşılaştırmak da faydalı olabilir. Yani, yamuğun hacmi de önemli bir konu.
Kürede Hacim Hesaplama
Evet Baykam, kürenin hacmini hesaplamak oldukça ilginç bir süreç. Kürenin hacmi, yarıçapı kullanarak hesaplanır ve formülü V = (4/3)πr³ olarak bilinir. Burada r, kürenin yarıçapıdır. Kürenin hacmini bulmak, hem matematiksel hem de fiziksel kavramları anlamayı kolaylaştırır.
Diğer Geometrik Şekillerle Karşılaştırma
Kürelere ek olarak, farklı geometrik şekillerin hacimlerini de incelemek faydalı olacaktır. Örneğin, yamuğun hacmi hesaplanırken farklı formüller kullanılır. Bu tür karşılaştırmalar, farklı geometrik şekillerin hacimlerinin nasıl değiştiğini anlamamıza yardımcı olur. Geometrik şekillerin hacim hesaplamalarını öğrenmek, matematiğin temel taşlarından biridir ve günlük hayatta da önemli bir yer tutar.
Kürede hacim hesaplamaları yaparken, yarım küre hacmi ile ilgili sorular da sıkça karşımıza çıkıyor. Örneğin, yarıçapı 10 cm olan bir yarım kürenin hacmini bulmak oldukça ilgi çekici. Bu tür sorular matematiksel becerimizi geliştirirken, hacim kavramını da daha iyi anlamamıza yardımcı oluyor.
Yarım Küre Hacmi Hesaplama
Kabil, yarım küre hacmi hesaplamaları gerçekten de hem matematiksel becerilerimizi geliştirmek hem de hacim kavramını anlamak için oldukça faydalıdır. Yarım kürenin hacmini bulmak için kullanılan formül şu şekildedir:
Hacim = (2/3) π r³
Burada 'r', yarım kürenin yarıçapını temsil eder. Örneğin, yarıçapı 10 cm olan bir yarım küre için hacmi hesaplamak istiyoruz.
Hacim = (2/3) π (10 cm)³
= (2/3) π 1000 cm³
≈ 2093.33 cm³ (π ≈ 3.14 alındığında)
Bu tür hesaplamalar, hem teorik bilgimizi pekiştirir hem de pratikte uygulama yapma fırsatı sunar. Özellikle geometri ve hacim konularında pratik yapmak, ileride daha karmaşık matematiksel problemleri çözme yeteneğimizi de artırır. Yarım küre hacmi gibi örnekler, öğrendiklerimizi pekiştirmenin yanı sıra, matematiksel düşünme becerimizi geliştirmek için de harika bir yoldur.
Kürecik hacim formülü ile ilgili bilgi sahibi olmak benim için çok faydalı oldu. Yarıküre hacim formülü de oldukça ilginç. Özellikle 60 derecelik küre dilimi hesaplaması yaparken yarıçapı kullanarak hacmi bulmak, matematiğin pratik uygulamalarından biri. Hem teorik hem de pratik açıdan önemli bir konu.
Kayyum,
Kürecik Hacim Formülü ile ilgili bilgi edinmenizin faydalı olduğunu duymak sevindirici. Matematikte hacim hesaplamaları, özellikle kütle ve alan gibi diğer fiziksel kavramlarla ilişkilendirildiğinde oldukça önemli bir yere sahip. Yarıküre Hacim Formülü de, hacim hesaplamalarında sıkça kullanılan bir formül olup, çeşitli uygulamalarda karşımıza çıkıyor.
60 Derecelik Küre Dilimi Hesaplaması yaparken yarıçap kullanarak hacmi bulmanız, matematiğin pratikteki uygulanabilirliğini gösteriyor. Bu tür hesaplamalar, günlük yaşamda ve mühendislik gibi alanlarda oldukça işlevsel hale geliyor. Hem teorik hem de pratik açıdan önemli bir konu üzerinde durmanız, matematiğin bu yönünü keşfetmeniz açısından çok değerli.
Bu konuda daha fazla bilgi edinmek isterseniz, her zaman yardımcı olmaktan memnuniyet duyarım.
Kürenin hacmini hesaplamaya çalışıyorum ama formüle yeterince hakim değilim. V = (4/3) Ï r³ formülünü kullanarak bir örnek çözebilir misiniz? Mesela yarıçapı 7 cm olan bir kürenin hacmini nasıl hesaplayabilirim?
Ece Su hanım, kürenin hacmini hesaplamanıza yardımcı olayım. Verdiğiniz formül olan V = (4/3) àró doğru. Yarıçapı 7 cm olan bir kürenin hacmini hesaplamak için bu formülü kullanacağız.
Önce r'nin (yarıçap) 7 cm olduğunu formüle yerleştirelim:
V = (4/3) à(7 cm)ó
7 cm'nin kübünü alalım:
7 cm × 7 cm × 7 cm = 343 cmó
Şimdi bu değeri formülde yerine koyalım:
V = (4/3) à× 343 cmó
Pi (ÃÂ) değerini yaklaşık olarak 3.14 olarak alalım:
V = (4/3) × 3.14 × 343 cmó
Bu hesaplamayı yaparsak:
V = (4/3) × 1076.02 cmó
V = 1434.69 cmó
Yani, yarıçapı 7 cm olan bir kürenin hacmi yaklaşık olarak 1434.69 cmó'dür. Umarım yardımcı olabilmişimdir!