Kürenin Yüzey Alanı Formülü Nelerdir?

Kürenin Yüzey Alanı Formülü

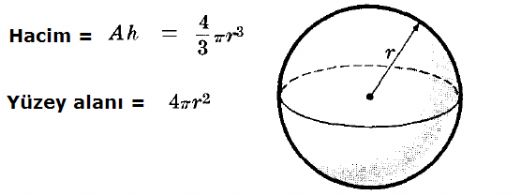
Kürenin Yüzey Alanı Formülü, Küre matematiğin alt dallarından biri olan geometri konusuna aittir. Küre sabit bir noktadan kendisine eşit uzaklıkta bulunan noktaların oluşturduğu bir cisimdir. Küre kusursuz simetriye ve ahenge sahip geometrik bir şekildir. Küreyi diğer geometrik şekillerden ayıran en önemli özellik uzunluğu, genişliği ve yüksekliği olmayışıdır. Kürenin sadece yarıçapı vardır. Merkez noktası ise "O" harfi ile gösterilir. Bir küre merkez doğrusu boyunca kesilirse yarıçap elde edilir. Kürenin merkez noktasından geçen ve bu nokta ile bitiş noktasını birleştiren doğruya ise kürenin çapı denir. Yarıçap "r" ifadesi ile çap ile "d" ifadesiyle gösterilir. Yarıçap sayesinde küreye ait tüm formüller bulunur. Kürenin kirişi küre yüzeyi üzerinde belirlenmiş herhangi iki noktayı birleştiren bir doğrudur. Küre yüzeyinin üzerinde bulunan ve çapı, kürenin çapına eşit olan çembere de kürenin çevrel çemberi denir. Küre çevrel çember boyunca kesildiğinde ortaya iki eşit parça çıkar. Bun parçaların tüm özellikleri birbirine eştir ve her ikisi de yarı küre olarak anılır.

Kürenin yüzey alanı

Yarıçapı r uzunlukta olan bir kürenin yüzey alanı yarıçapın alanının 4 katına eşittir.

A = 4.π.r2

Kürenin kesit alanı

Ak = π.r2

Kürenin hacmi

V = 4/3 * (π. r3 )

Kürenin kesit alanının hacme oranı

Ak/V = 3/4r

Kürenin yüzey alanının hacme oranı

A/V = 3/r

Kürenin herhangi bir parçasının hacmi

Vks = [(h2.π)/3 * (3r-h)]

Son Güncelleme : 17.12.2020 04:15:31

Kürenin Yüzey Alanı Formülü ile ilgili bu madde bir taslaktır. Madde içeriğini geliştirerek Herkese açık dizin kaynağımıza katkıda bulunabilirsiniz.

Yemek Sodası Formülü

Yemek sodası formülü, yemek sodası olarak bilinen sodyum bikarbonat, beyaz toz, kristal halde bulunan sodyum tuzlarından bir tanesidir. Mutfak hayatımızın içerisinde sürekli kullanmış olduğumuz sodyum bikarbonat hanımlar arasında kabartma tozu olarak...

Permanganat Formülü

Permanganat Formülü; Kristal yapıda olan tuz koyu menekşe rengine sahiptir. Permanganat klor bileşiğinin potasyum manganat ile tepkimeye girmesi sonucunda elde edilmektedir. Permanganat su ile tepkimeye girerek menekşe rengini vermektedir. Menekşe re...

Basınç Kuvveti Formülü

Basınç kuvveti; basınç; birim yüzeye etki eden dik kuvvetin oluşturduğu etkiye denir. Basıncın formülü;Basınç= Kuvvet/ AlanBasınç: P (N/m2) (Pascal) (Pa)Kuvvet: F (Newton) (N)Alan: S (metrekare) (m2) ve P=F/S şeklinde alınır.Katılarda basınç ve basın...

Nişasta Formülü

Nişasta Formülü; nişasta suda çözünmesi mümkün olmayan karmaşık bir karbonhidrat türüdür. Nişasta beyaz, kokusuz ve tatsız bir toz türüdür. Bitkiler nişastayı fazla olan glikozu depolamak için kullanmaktadırlar. Sanayilerde tutkal, kağıt ve tekstil i...

İş Formülü

İş Formülü; iş; bilimsel anlamda cismin bir kuvvetin etkisinde yol alması yada yer değiştirmesi olayıdır. Yani bir olayın iş olabilmesi için alınması gereken bir yol ve kuvvet gereklidir. İş, skaler bir büyüklüktür.Kuvvet yer değiştirme doğrultusunda...

Diyoptri Formülü

Diyoptri Formülü, optik biliminde bir aynanın yada bir merceğin optiksel gücünü yani ışığı kırabilme gücünü bulmaya yarayan formüldür. Aynanın veya merceğin odak mesafesinin tersi şeklinde ifade edilmektedir. Simgesel olarak f: odak mesafesi o...

Şap Formülü

Şap formülü; şap çift tuz grubuna giren bileşiklerdir. Şap suda kolaylıkla çözülebilen tatlımsı bir tadı olan bir bileşiktir. Hava ile temasında ise kararır. Şap formülü Me+1Me+3(SO4)subrast2.12H2O şeklindedir. Buradaki Me+1=K+, NH4+, Rb+, Cs+, TI+ ...

Kütle Formülü

Kütle formülü, fizik biliminin bir konusudur ve adından da anlaşılacağı gibi cismin kütlesini bulmaya yarar. Öncelikle kütle, değişmeyen madde miktarıdır. Peki bu ne demek? Yani bir cismin sahip olduğu madde miktarının dünyanın her yerinde aynı olmas...

Manganat Formülü

Manganat Formülü; Manganat anyonik bir köktür. Manganatın sembolü (MnO4)-2 şeklindedir ve buradaki - yükü anyon olduğunu gösterir. Manganat katyonlar ile bileşik oluşturma özelliğine sahiptir. Atom numarası 25, sembolü Mn olan bir tane Mangan yada M...

İtme Formülü

İtme formülü; bir cisme uygulanan net kuvvet, cismin hem hızını değiştirir hem de cismin ivmeli harekete etmesini sağlar. Cisme etki eden net kuvvet ve kuvvetin etki etme süresinin çarpımına itme diğer adı impuls denir. İtme formülü; İtme= net kuvvet...

Kromat Formülü

Kromat Formülü, Kromat, oksijen ile sodyunmdan elde edilen iyonik niteliğe sahip olan inorganik bir bileşiktir. Kromat bileşiğin ayrıca rakromat, disodyum tuzu ve disodyum oksit adları ile de bilinmektedir. Su ile tepkimeye giren kromat iyonlara ayrı...

Nitrür Formülü

Nitrür Formülü; Nitrür bir azot elementinin (N) anyonik şeklidir. Nitrürün sembolü N-3 şeklinde olur. Buradaki -3 yükü anyon olduğunu gösterir. Nitrür önemli anyonlar arasında yer alır. Nitrür hem katyonlar ile hem de bazı kimyasal kökler ile bileşik...

Kürenin Yüzey Alanı Formülü

Kürenin Yüzey Alanı Formülü Yorumları