
Alan Formülleri Nelerdir?
Bu içerik, geometrik şekillerin alan hesaplamalarıyla ilgili temel formülleri ve örnekleri içermektedir. Dikdörtgen, kare, üçgen, daire, paralelkenar ve trapez gibi şekillerin alanları nasıl hesaplanır, açıklayıcı bir şekilde ele alınmıştır. Alan hesaplamalarının önemi de vurgulanmaktadır.
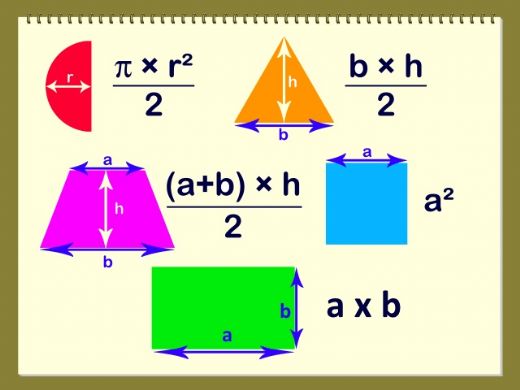
Alan, bir iki boyutlu şeklin kapladığı yüzeyin ölçüsünü ifade eden bir kavramdır. Matematik ve geometri alanında, çeşitli şekillerin alanını hesaplamak için kullanılan formüller mevcuttur. Bu makalede, farklı geometrik şekillerin alan hesaplamalarını inceleyeceğiz. 1. Dikdörtgenin Alanı Dikdörtgen, iki çift paralel kenardan oluşan bir geometrik şekildir. Alanı, uzun kenar ile kısa kenarın çarpımı ile hesaplanır.
Örneğin, uzun kenarı 5 cm ve kısa kenarı 3 cm olan bir dikdörtgenin alanı 15 cm²'dir. 2. Karenin Alanı Kare, tüm kenar uzunlukları eşit olan bir dikdörtgendir. Alanı, bir kenarın uzunluğunun karesi alınarak hesaplanır.
Örneğin, bir kenarı 4 cm olan bir karenin alanı 16 cm²'dir. 3. Üçgenin Alanı Üçgen, üç kenarı ve üç açısı olan bir geometrik şekildir. Alanı, taban uzunluğu ile yükseklik uzunluğunun çarpımının yarısı alınarak hesaplanır.
Örneğin, tabanı 6 cm ve yüksekliği 4 cm olan bir üçgenin alanı 12 cm²'dir. 4. Dairenin Alanı Daire, merkez etrafında eşit uzaklıkta bulunan noktaların oluşturduğu bir şekildir. Dairenin alanı, pi sayısı (π) ile dairenin yarıçapının karesinin çarpımı ile hesaplanır.
Örneğin, yarıçapı 3 cm olan bir dairenin alanı yaklaşık 28.27 cm²'dir (π ≈ 3.14). 5. Paralelkenarın Alanı Paralelkenar, iki çift paralel kenar ve eşit uzunlukta olan kenarları içeren bir geometrik şekildir. Alanı, taban uzunluğu ile yükseklik uzunluğunun çarpımı ile hesaplanır.
Örneğin, tabanı 8 cm ve yüksekliği 5 cm olan bir paralelkenarın alanı 40 cm²'dir. 6. Trapezinin Alanı Trapez, bir çift kenarı paralel olan dörtgenlerdir. Alanı, paralel kenarların toplamının yarısı ile yükseklik uzunluğunun çarpımı ile hesaplanır.
Örneğin, üst kenarı 5 cm, alt kenarı 7 cm ve yüksekliği 4 cm olan bir trapezinin alanı 24 cm²'dir. Ekstra Bilgiler Geometrik şekillerin alan hesaplamaları, mühendislik, mimarlık ve çeşitli bilimsel alanlarda büyük öneme sahiptir. Alan hesaplamaları, malzeme kullanımı, inşaat projeleri ve çevresel analizlerde sıklıkla kullanılmaktadır. Ayrıca, alan formülleri, matematiksel düşünme becerilerini geliştirmek ve problem çözme yeteneklerini artırmak için eğitim alanında da kullanılmaktadır. Sonuç olarak, alan formülleri, geometrik şekillerin alanını hesaplamak için temel bir araçtır. Bu formüller, matematiksel kavramların daha iyi anlaşılmasına yardımcı olmakta ve çeşitli pratik uygulamalarda önem taşımaktadır. Her bir şekil için farklı formüller mevcut olup, bu formüllerin doğru bir şekilde uygulanması, alan hesaplamalarında kesin sonuçlar elde edilmesini sağlamaktadır. |















































Dikdörtgenin alan formülünü öğrenmek istiyorum ama neden iç açıları toplamı 360 derece? Dikdörtgenin kısa kenarı ve uzun kenarı nasıl belirlenir?
Merhaba Tuzun,
Dikdörtgenin alan formülü, kısa kenar ile uzun kenarın çarpılmasıyla bulunur: Alan = Kısa Kenar x Uzun Kenar. Dikdörtgenin iç açılarının toplamının 360 derece olması, geometrik bir özelliktir ve tüm dörtgenler için geçerlidir. Bir dikdörtgende her bir iç açı 90 derecedir ve 4 x 90 = 360 derece eder.
Kısa kenar ve uzun kenar, dikdörtgenin kenar uzunluklarına göre belirlenir. En kısa kenar "kısa kenar", en uzun kenar ise "uzun kenar" olarak adlandırılır. Dikdörtgenin karşılıklı kenarları birbirine eşittir, yani iki kısa kenar ve iki uzun kenar bulunur. Bu nedenle kenar uzunluklarını ölçerek kısa ve uzun kenarları kolayca belirleyebilirsin.
Umarım yardımcı olabilmişimdir.
Sevgiler,