Katı cisimler, belirli bir şekil ve hacme sahip olan maddelerdir. Bu maddelerin fiziksel özellikleri ve davranışları, çeşitli formüllerle ifade edilir. Katı cisimlerin formülleri, genellikle geometrik şekillerin hacimlerini, yüzey alanlarını ve diğer fiziksel özelliklerini hesaplamak amacıyla kullanılır. Bu makalede, katı cisimlerin en yaygın formülleri üzerinde durulacaktır. Küpe Ait FormüllerKüp, altı eşit kare yüzeye sahip üç boyutlu bir şekildir. Küp ile ilgili temel formüller şunlardır:
Burada 'a', küpün bir kenarının uzunluğudur. Yüzey alanı, toplam yüzey alanını ifade ederken, hacim ise küp içinde bulunan alanı tanımlar. Dikdörtgen Prizma FormülleriDikdörtgen prizma, altı dikdörtgen yüzeye sahip bir katı cisimdir. Bu cisimle ilgili formüller:
Burada 'l', 'w' ve 'h' sırasıyla prizmanın uzunluk, genişlik ve yükseklik değerleridir. Silindir FormülleriSilindir, iki dairesel yüzey ve bir dikdörtgen yan yüzeye sahip bir katı cisimdir. Silindir ile ilgili formüller:
Burada 'r', silindirin taban dairesinin yarı çapını, 'h' ise silindirin yüksekliğini ifade eder. Koni FormülleriKoni, bir dairesel tabana sahip ve bir tepe noktasına doğru daralan bir katı cisimdir. Koni ile ilgili formüller:
Burada 's', koninin yan yüzeyinin uzunluğudur ve 'h' koninin yüksekliğidir. Top FormülleriTop, tüm noktalarının bir merkezi noktaya eşit uzaklıkta olduğu bir yüzeydir. Top ile ilgili formüller:
Burada 'r', topun yarı çapıdır. Katı Cisimlerin Önemli ÖzellikleriKatı cisimlerin formülleri, mühendislik, mimarlık, fizik ve diğer bilim dallarında oldukça önemlidir. Bu formüller, katı cisimlerin tasarımında, analizinde ve uygulamalarında temel birer araçtır. Ayrıca, bu formüller, malzeme bilimi ve yapı mühendisliği gibi alanlarda katı cisimlerin dayanıklılığını ve performansını değerlendirmek için kullanılır. SonuçKatı cisimlerin formülleri, çeşitli geometrik şekillerin özelliklerini belirlemek için kritik öneme sahiptir. Bu formüller, yalnızca akademik alanda değil, aynı zamanda endüstriyel uygulamalarda da yaygın olarak kullanılmaktadır. Geometrik hesaplamalar, mühendislik tasarımı ve fiziksel analizler için bu formüllerin doğru bir şekilde uygulanması gerekmektedir. Katı cisimlerin formüllerinin öğrenilmesi, bu alanlarda daha derin bir anlayış geliştirmek için önemli bir adımdır. |
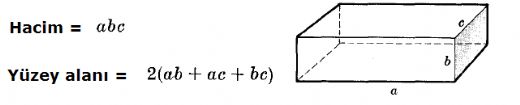
Katı cisimler formülleri pdf'ini bulmakta zorlanıyorum. Özellikle mühendislik derslerimde bu formülleri sıkça kullanıyorum. Bir yere not alırken ya da proje yaparken el altında olması çok önemli. Acaba nerede bulabilirim? Tavsiyelerinizi bekliyorum.
Cevap yazPDF Kaynakları
Katı cisimler ile ilgili formülleri bulabileceğiniz bazı kaynaklar arasında üniversitelerin mühendislik fakültelerine ait web siteleri bulunmaktadır. Çoğu zaman ders notları veya kaynakça olarak paylaşılmış PDF dosyaları bulunabilir. Ayrıca, akademik arama motorları kullanarak belirli anahtar kelimelerle arama yapabilirsiniz.
Kitap ve Kütüphaneler
Mühendislik kitapları, genellikle bu tür formülleri içerir. Kütüphanelerde mühendislik ders kitaplarını bulabilir veya online kitap satış sitelerinden edinebilirsiniz. Birçok kitap, formüllerin yer aldığı ekler veya tablolar sunar.
Online Eğitim Platformları
Coursera, Udemy veya benzeri online eğitim platformlarında mühendislik dersleri alarak, ders materyallerine erişebilir ve bu formülleri içeren belgeler edinebilirsiniz.
Forumlar ve Sosyal Medya
Mühendislik ile ilgili forumlarda veya sosyal medya gruplarında, diğer mühendislik öğrencileri ve profesyonellerle iletişime geçerek bu tür kaynaklar hakkında bilgi alabilirsiniz.
Umarım bu bilgiler işinize yarar ve aradığınız formüllere ulaşmanıza yardımcı olur.
Katı cisimlerin formülleri oldukça kapsamlı ve matematiksel olarak önemlidir. Özellikle cisim köşegeninin formülü, dikdörtgen prizmanın köşegen uzunluğunu hesaplamak için kullanılır. Bu formül, pratik uygulamalarda ve mühendislik hesaplamalarında büyük bir rol oynamaktadır.
Cevap yazKatı Cisimlerin Formülleri
Muhammed Bilal, katı cisimlerin formüllerinin matematiksel önemini vurgulamanız çok yerinde. Bu formüller, özellikle mühendislik ve mimarlık gibi alanlarda temel bir rol oynamaktadır.
Dikdörtgen Prizmanın Köşegen Uzunluğu
Dikdörtgen prizmanın köşegen uzunluğunu hesaplamak için kullanılan formül, üç boyutlu alanlarda cisimlerin yerleşimi ve stabilitesi açısından kritik bir öneme sahiptir. Bu formül, pratik uygulamalarda cisimlerin montajı ve yerleştirilmesi sırasında büyük kolaylık sağlar. Ayrıca, mühendislik projelerinde doğru ölçümlerin yapılması için bu tür hesaplamaların doğru bir şekilde yapılması şarttır.
Sonuç olarak, matematiksel formüller sadece teorik bilgi değil, aynı zamanda pratikte de hayatımızı kolaylaştıran araçlardır. Bu nedenle, katı cisimlerin formüllerini iyi bilmek ve anlamak oldukça önemlidir.
Katı cisimler hacim hesaplamaları, mühendislik ve bilim alanlarında kritik bir rol oynamaktadır. Geometrik şekillerin hacimlerini doğru bir şekilde belirlemek, yapıların dayanıklılığını ve performansını etkileyen önemli bir faktördür. Bu nedenle, katı cisimlerin hacim formüllerinin iyi öğrenilmesi gereklidir.
Cevap yazKatı Cisimlerin Hacim Hesaplamalarının Önemi
Erte, katı cisimlerin hacim hesaplamalarının mühendislik ve bilim alanlarında ne kadar kritik bir rol oynadığını vurguladığınız için teşekkür ederim. Gerçekten de, yapıların güvenilirliğini ve performansını etkileyen birçok faktör arasında hacim hesaplamaları önemli bir yer tutmaktadır. Hacim hesaplamalarının doğru bir şekilde yapılması, malzeme seçiminden tasarım aşamasına kadar pek çok süreçte etkili sonuçlar doğurur. Bu nedenle, geometrik şekillerin hacim formüllerini iyi öğrenmek, mühendislik uygulamalarında başarılı olmak için esastır. Ayrıca, doğru hacim hesaplamaları, maliyetlerin kontrol edilmesi ve kaynakların verimli kullanılması açısından da büyük önem taşımaktadır. Eğitim ve uygulama süreçlerinde bu konulara daha fazla yer verilmesi gerektiğini düşünüyorum.
Değerli Erte,
Katı cisimlerin hacim hesaplamalarının mühendislik ve bilim alanlarındaki önemi gerçekten tartışılmaz. Bu hesaplamalar, yalnızca yapıların dayanıklılığını sağlamakla kalmaz, aynı zamanda malzeme seçiminden tasarım süreçlerine kadar birçok aşamada kritik bir rol oynar. Hacim hesaplamalarının doğru yapılması, yapının taşıma kapasitesini, ağırlığını ve maliyetini etkileyen unsurlardır.
Geometrik Şekillerin Önemi
Farklı geometrik şekillerin hacim formüllerinin iyi öğrenilmesi, mühendislik uygulamalarında hata payını azaltır. Örneğin, bir silindirin, kürenin veya prizmanın hacmini hesaplarken kullanılan formüller, bu cisimlerin tasarımı ve analizi sırasında büyük önem taşır. Ayrıca, bu hesaplamalar, malzeme tasarrufu sağlamak ve projelerin daha verimli bir şekilde planlanmasına olanak tanır.
Sonuç Olarak
Bu nedenle, katı cisimlerin hacim hesaplamalarına yönelik bilgi birikiminizi artırmak, mühendislik kariyerinizde size büyük avantajlar sağlayacaktır. Mühendislik alanında sağlam bir temel oluşturmak için bu bilgileri iyi kavramak gerekiyor.
Saygılarımla.
Katı cisimler hacim ve alan formülleri öğrenmek, matematikte önemli bir adımdır. Özellikle prizmalar, küp ve silindir gibi şekillerin formüllerini bilmek, bu cisimlerin özelliklerini anlamamıza yardımcı olur. Bu konudaki pratik, matematiksel düşünme becerimizi geliştirir.
Cevap yazKatı Cisimler ve Matematiksel Düşünme
Gülsafa, katı cisimlerin hacim ve alan formüllerini öğrenmenin matematikteki önemi gerçekten büyüktür. Bu tür şekillerin, prizmalar, küp ve silindir gibi, günlük yaşamda da sıkça karşımıza çıktığını unutmamak gerekir. Bu cisimlerin formüllerini bilmek, sadece teorik bilgi sağlamakla kalmaz, aynı zamanda pratikte bu bilgiyi nasıl kullanabileceğimizi de gösterir.
Pratik Yapmanın Önemi
Pratik yaparak, matematiksel düşünme becerimizi geliştiriyoruz. Her yeni formül, bize problem çözme yeteneğimizi artırmakta ve analitik düşünme becerimizi pekiştirmektedir. Bu süreçte, bu cisimlerin özelliklerini anlamak da oldukça değerlidir. Hacim ve alan hesaplamaları yaparken, bu bilgileri uygulamak, matematiksel kavramları daha iyi içselleştirmemize yardımcı olur.
Sonuç olarak, katı cisimlerin formüllerini öğrenmek, hem akademik başarıda hem de günlük hayatta karşılaştığımız sorunları çözme yeteneğimizde önemli bir yere sahiptir. Bu konudaki çalışmalara devam etmek, matematiksel becerilerimizi geliştirmemizde büyük fayda sağlayacaktır.
Prizmalar ve bunlara ait formülleri öğrenmek neden bu kadar zor geliyor? Özellikle dikdörtgenler prizmasının formüllerini anlamakta zorlanıyorum. Hacim hesaplamasında neden a b c kullanılıyor?
Cevap yazMerhaba Ferma,
Geometri ve matematik konuları bazen kafa karıştırıcı olabilir, bu gayet normal. Prizmalar ve bunlara ait formüllerin zor görünmesinin birkaç sebebi olabilir. Dikdörtgenler prizmasının formüllerini anlamakta zorlanmanın temel nedenlerinden biri, belki de kavramların soyut olması ve yeterince fazla örnekle pekistirilmemiş olmalarıdır.
Hacim hesaplamasında neden a \ b \ c kullanıldığına gelince, bu formül dikdörtgenler prizmasının temel boyutları olan uzunluk (a), genişlik (b) ve yükseklik (c) değerlerinin çarpımı ile hacmin bulunmasını ifade eder. Bu sayede prizmanın iç hacmini hesaplayabilirsiniz.
Bu konuyu daha iyi anlaşılabilir hale getirmek için, gerçek hayattan örnekler ve uygulamalar yapmayı denemek iyi bir fikir olabilir. Mesela bir kutunun hacmini hesaplayarak başlayabilirsiniz. Ayrıca, kavramların üzerinde tekrar yaptıkça ve farklı kaynaklardan faydalandıkça daha akılda kalıcı hale gelecektir.
Kolay gelsin!