
Kök Bulma Formülü Nelerdir?
Kök bulma formülü, matematikte bir sayının karekökü, küpkökü veya n'inci kökünü hesaplamak için kullanılan yöntemleri ifade eder. Bu işlemler, bilimsel hesaplamalarda ve mühendislikte kritik bir rol oynar. Kök bulma yöntemleri, doğru sonuçlar elde etmede önemlidir.
Kök Bulma Formülü Nedir?Kök bulma formülü, matematikte bir sayının karekökünü, küpkökünü veya genel olarak n'inci kökünü hesaplamak için kullanılan yöntemlerdir. Bu formüller, genellikle cebirsel hesaplamalarda ve çeşitli bilimsel uygulamalarda önemli bir rol oynamaktadır. Kök bulma işlemi, sayısal analizde ve mühendislikte sıkça karşılaşılan bir problemdir. Karekök Bulma Karekök, bir sayının kendisiyle çarpıldığında verilen sayıyı veren sayıdır. Karekök bulma işlemi genellikle şu formülle ifade edilir:
Bu formülde "√" sembolü, karekökü temsil eder ve x sayısının karekökü y olarak tanımlanır. Karekök, pozitif bir sayı için iki değer alabilir; ancak genellikle pozitif değeri tercih edilir. Küpkök Bulma Küpkök, bir sayının kendisiyle üç kez çarpıldığında verilen sayıyı veren sayıdır. Küpkök bulma işlemi, aşağıdaki formülle ifade edilir:
Bu formülde "∛" sembolü, küpkökü temsil eder. Küpkök, herhangi bir reel sayı için bir değer alır. Genel n'inci Kök Bulma Formülü Bir sayının n'inci kökünü bulmak için genel formül şu şekildedir:
Bu formülde "x" sayısının n'inci kökünü bulmak için x sayısı, "n" pozitif bir tam sayı olmak üzere tanımlanır. Kök Bulma Yöntemleri Kök bulma işlemleri çeşitli yöntemlerle gerçekleştirilebilir. İşte bu yöntemlerden bazıları:
Kök Bulma Uygulamaları Kök bulma formülleri, çeşitli bilim dallarında ve mühendislik uygulamalarında yaygın olarak kullanılmaktadır. Bu uygulamalardan bazıları şunlardır:
Sonuç Kök bulma formülleri, matematiksel hesaplamaların temel unsurlarından biridir ve birçok alanda uygulama bulmaktadır. Karekök, küpkök ve genel n'inci kök hesaplamaları, bilimsel ve mühendislik çalışmalarında kritik bir rol oynamaktadır. Kök bulma yöntemlerinin doğru ve etkili bir şekilde uygulanması, doğru sonuçlar elde edilmesini sağlamaktadır. |
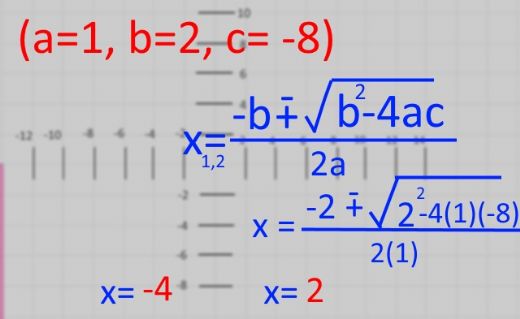















































Kök delta bölü mutlak a ifadesi, matematiksel hesaplamalarda önemli bir yer tutar. Kök bulma işlemlerinde delta'nın etkisi, sonuçların doğruluğunu artırır. Bu tür hesaplamalarda mantıklı ve sistematik bir yaklaşım sergilemek, karmaşık problemleri daha anlaşılır hale getirir.
Değerli Yorumunuz İçin Teşekkürler
Azad, kök delta bölü mutlak a ifadesinin matematikteki önemi gerçekten büyüktür. Bu tür matematiksel kavramlar, özellikle karmaşık hesaplamalar yaparken sonuçların doğruluğunu artırmada kritik bir rol oynar. Kök bulma işlemlerinde delta'nın etkisini anlamak, süreçleri daha yönetilebilir hale getirir.
Ayrıca, sistematik bir yaklaşım benimsemek, hem öğrenme sürecinde hem de uygulama aşamasında büyük fayda sağlar. Mantıklı bir şekilde ilerlemek, matematiğin soyut yapısını daha anlaşılır kılmaktadır. Bu tür düşünceler, matematiksel becerilerin gelişimine de katkıda bulunur. Yorumunuz bu konudaki farkındalığı artırdığı için takdir ediyorum.
Kök bulma formülü ile ilgili bu bilgileri okuduktan sonra, ikinci derece denklemlerin köklerini bulmak için delta formülünü kullanmanın ne kadar önemli olduğunu anlıyoruz. Özellikle farklı durumlar için köklerin belirlenmesi, matematikteki problemlerin çözümünde büyük kolaylık sağlıyor. Mesela, delta formülünü kullanarak kökleri bulmak için işleme soldan formülü ile başlamak gerektiğini unutmayalım. Bu yöntem, denklemlerin köklerini bulma sürecinde oldukça etkili ve sistematik bir yaklaşım sunuyor.
Berk,
Kök Bulma Formülü ve Delta Formülü hakkında verdiğin bilgiler oldukça aydınlatıcı. İkinci derece denklemlerin köklerini bulmak için delta formülünün önemi gerçekten büyük. Bu yöntem, karmaşık problemlerde bile sistematik bir çözüm sunarak matematiksel süreçleri daha anlaşılır hale getiriyor.
Köklerin Belirlenmesi aşamasında, delta değerinin hesaplanması, denklemin köklerinin gerçek mi yoksa karmaşık mı olduğunu belirlemede kritik bir adım. Farklı durumlar için köklerin belirlenmesi, matematiksel problemlerin çözümünde sağladığı kolaylık sayesinde, hem öğrencilerin hem de profesyonellerin işini kolaylaştırıyor.
Bu noktada, formülü soldan başlatarak uygulamak, adım adım ilerlemek açısından önemli bir strateji. Böylece, her aşamada ne yaptığınızı bilerek ilerleyebilir ve olası hataların önüne geçebilirsiniz. Sonuç olarak, delta formülünün kullanımı, matematikte kök bulma sürecini daha verimli ve anlaşılır kılıyor.
Teşekkürler!
Negatif olmayan bir sayının karekökünü bulma işlemi neden önemli? Kareköklü sayılarla günlük hayatta nerelerde karşılaşabiliriz?
Tanay, karekök hesaplama işlemi birçok alanda oldukça önemlidir. Özellikle mühendislik, mimarlık ve bilgisayar bilimleri gibi alanlarda sıkça kullanılır. Örneğin, bir binanın yüksekliğini veya bir nesnenin boyutlarını hesaplamak için karekök kullanmak gerekebilir. Ayrıca, finansal analizlerde ve istatistiklerde de karekök işlemleri önemli bir yer tutar. Günlük hayatta ise mesafeleri, zamanları ve hızları hesaplarken karekök işlemiyle karşılaşabiliriz. Kısacası, karekök hesaplaması hem teorik hem de pratik birçok alanda karşımıza çıkar ve matematiksel analizlerin temel taşlarından biridir.