
İntegral Formülleri Nelerdir?
İntegral formülleri, matematiksel analizde alan ve hacim hesaplamalarında kullanılan önemli yöntemlerdir. Bu yazıda, belirli ve belirsiz integral türleri, temel integral formülleri ve hesaplama teknikleri ele alınarak, integralin çeşitli uygulama alanlarına değinilecektir.
İntegral formülleri, matematiksel analizde önemli bir yere sahip olan integral hesaplamalarını kolaylaştıran ve belirli bir alanı veya hacmi bulmak için kullanılan yöntemlerdir. İntegral, bir fonksiyonun altındaki alanı veya bir nesnenin hacmini belirlemek için kullanılan bir hesaplama aracıdır. Bu makalede, integral formüllerinin çeşitleri, uygulama alanları ve bazı önemli özellikleri üzerinde durulacaktır. İntegral Türleri İntegraller, genel olarak iki ana başlık altında incelenebilir: belirli integral ve belirsiz integral.
İntegral Formülleri Aşağıda, bazı temel integral formülleri listelenmiştir:
İntegral Hesaplama Teknikleri İntegral hesaplamaları genellikle bazı teknikler ve yöntemler kullanılarak gerçekleştirilir. Bu tekniklerden bazıları şunlardır:
Uygulama Alanları İntegral formülleri, birçok alanda uygulama bulur:
Sonuç İntegral formülleri, matematiğin temel taşlarından birini oluşturarak, birçok bilim dalında uygulama alanı bulmaktadır. Belirli ve belirsiz integrallerin yanı sıra, çeşitli teknik ve yöntemlerle hesaplama yapılması, matematiksel analizde önemli bir yer tutmaktadır. Bu nedenle, integral formüllerinin öğrenilmesi ve uygulama alanlarının anlaşılması, matematiksel yetkinlik açısından büyük önem taşımaktadır. |
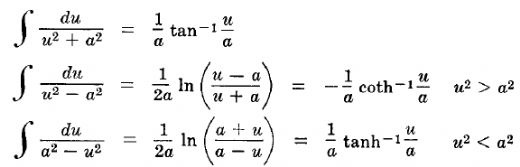















































Matematikle ilgili bu bilgilere dayanarak, integral ve türev arasındaki ilişkiyi tam olarak kavrayabilmek için hangi noktaların daha fazla üzerinde durulması gerektiğini düşünüyorsun? Özellikle integral alma yöntemleri arasında hangisinin daha karmaşık olduğunu ve nedenini merak ediyorum. Ayrıca, bu yöntemlerin gerçek dünyada nasıl uygulandığını görmek de oldukça ilginç değil mi? Örneğin, mühendislik veya fizik alanında integralin nasıl kullanıldığına dair bir örnek verebilir misin?
Integral ve Türev Arasındaki İlişki
Integral ve türev arasındaki ilişki, matematikteki en temel kavramlardan biridir. Öncelikle, türev bir fonksiyonun anlık değişim oranını gösterirken, integral bu değişimlerin toplamını temsil eder. Bu nedenle, bu iki kavramın temel tanımlarını çok iyi anlamak önemlidir. Ayrıca, Fundamental Theorem of Calculus (Kalkülüsün Temel Teoremi) üzerinde durmak, bu iki kavramın nasıl birbirini tamamladığını kavramak açısından faydalı olacaktır.
Integral Alma Yöntemleri
Integral alma yöntemleri arasında bazıları daha karmaşık olabilir. Özellikle, parçalı integrasyon ve değişken değiştirme yöntemleri başlangıçta zorlayıcı olabilir, çünkü her iki yöntem de belirli bir düzeyde yaratıcılık ve deneyim gerektirir. Ancak, bu yöntemlerin nasıl çalıştığını anladıkça, karmaşıklığı aşmak daha kolay hale gelir.
Gerçek Dünya Uygulamaları
Integralin mühendislik veya fizik alanındaki uygulamaları oldukça geniştir. Örneğin, bir cismin hareketini anlamak için, cismin hız fonksiyonunun integralini alarak, cismin belirli bir zaman aralığında aldığı mesafeyi bulabiliriz. Bu, özellikle kinematik problemlerinde sıkça kullanılan bir yöntemdir. Ayrıca, elektrik mühendisliğinde, bir devredeki enerji akışını hesaplamak için de integraller kullanılır. Bu tür uygulamalar, integralin gerçek dünya problemlerini çözmedeki önemini göstermektedir.