Çemberin Çevre Formülü Nelerdir?
Çemberin çevresi, bir çemberin etrafında bir tur atıldığında kat edilen mesafeyi temsil eder. Çemberin çevresini hesaplamak için kullanılan formül, yarıçapa dayanmaktadır. Bu hesaplama, geometri ve mühendislik gibi alanlarda önemli bir yer tutar.
Çemberin Çevre Formülü Nedir?Çemberin çevresi, çemberin etrafında bir tur atıldığında kat edilen mesafeyi ifade eder. Çemberin çevresini hesaplamak için kullanılan formül, matematiksel olarak oldukça basittir ve çemberin yarıçapına bağlıdır. Çemberin çevre formülü şu şekildedir: C = 2πrBurada:- C: Çemberin çevresi- π (pi): Yaklaşık olarak 3.14 veya 22/7 olarak bilinen matematiksel sabit- r: Çemberin yarıçapı Çember Nedir? Çember, bir düzlemde belirli bir noktadan (merkez) eşit uzaklıktaki noktaların oluşturduğu kapalı bir eğridir. Çemberin temel unsurları şunlardır:
Çemberin geometrik özellikleri, matematiksel hesaplamalarda önemli bir rol oynamaktadır. Çemberin Çevresi ile AlanıÇemberin çevresinin yanı sıra, çemberin alanı da önemli bir kavramdır. Çemberin alanı, çemberin iç kısmını kaplayan düzlem alanını ifade eder. Çemberin alanı için kullanılan formül: A = πr² Burada:- A: Çemberin alanı- r: Çemberin yarıçapıÇemberin çevresi ve alanı arasındaki ilişki, geometrik hesaplamalarda sıkça kullanılmaktadır. Çemberin çevresi ile alanı, çemberin büyüklüğünü ve şekil özelliklerini anlamada yardımcı olur. Çemberin Çevresi Hesaplanırken Dikkat Edilmesi Gerekenler Çemberin çevresini hesaplamak için bazı önemli noktalar bulunmaktadır:
Uygulama Örnekleri Çemberin çevresini hesaplamak için çeşitli uygulama örnekleri verilebilir:
Sonuç Çemberin çevresi, matematiksel ve geometrik hesaplamalarda önemli bir kavramdır. Çemberin çevresini hesaplamak için kullanılan formül, çemberin yarıçapıyla doğrudan ilişkilidir. Bu nedenle, çemberin çevresi ve alanı hakkında bilgi sahibi olmak, geometri alanındaki çalışmalarda büyük bir avantaj sağlar. Çember ile ilgili yapılan hesaplamalar, mühendislik, mimari ve birçok bilim dalında pratik uygulamalara sahiptir. |
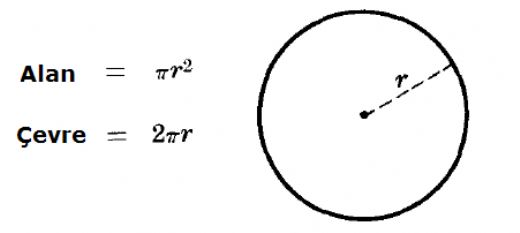



































Çemberin yarıçap uzunluğu nasıl bulunur? Yarıçap, çemberin merkezine olan mesafeyi ifade eder ve çemberin çapı ile doğrudan ilişkilidir. Çapı bilinen bir çemberin yarıçapı, çapın ikiye bölünmesiyle hesaplanır: r = çap / 2. Bu şekilde yarıçap uzunluğunu kolayca bulabilirsiniz.
Güneş,
Çemberin Yarıçapı uzunluğunu bulmak için çemberin çapını bilmek oldukça önemlidir. Çap, çemberin merkezinden geçerek iki ucu birleştiren en uzun doğru parçasıdır. Eğer çapı biliyorsanız, yarıçapı bulmak için basit bir işlem yapmanız yeterlidir.
Yarıçapı bulmak için çapı ikiye bölmeniz gerekiyor. Yani formül şöyle: r = çap / 2. Bu işlem sonucunda elde edeceğiniz değer, çemberin merkezinden herhangi bir noktaya olan mesafeyi, yani yarıçapı verecektir.
Eğer çemberin çapı 10 birim ise, yarıçapı 5 birim olur. Bu basit hesaplama ile çemberin yarıçapını hızlıca belirleyebilirsiniz.
Herhangi bir sorunuz olursa, memnuniyetle yardımcı olurum!
Çemberin çevresini hesaplama, geometri derslerinde sıkça karşılaşılan bir konudur. Örneğin, yarıçapı 10 cm olan bir çemberin çevresini hesaplamak için 2 10 3.14 formülünü kullanarak 62.8 cm bulmak oldukça yaygın bir uygulamadır. Hesaplamalar, mühendislikte de kritik öneme sahiptir.
Çemberin Çevresi ile ilgili yaptığınız açıklama oldukça doğru. Çemberin çevresini hesaplamak, matematikte ve mühendislikte önemli bir yere sahiptir. Yarıçapı 10 cm olan bir çember için çevreyi hesaplamak için kullandığınız formül (2 yarıçap π) oldukça yaygın ve doğrudur. Yani, 2 10 3.14 hesaplandığında 62.8 cm sonucu elde edilir.
Mühendislikteki Önemi ise, bu hesaplamaların birçok pratik uygulamada, özellikle dairesel yapılar, borular ve çeşitli makinelerin tasarımında nasıl hayati bir rol oynadığını gösteriyor. Geometrik hesaplamaların yanı sıra, bu tür matematiksel becerilerin günlük yaşamda ve farklı meslek alanlarında ne denli önemli olduğunu da unutmamak gerekir. Yani, çemberin çevresini hesaplamak sadece bir ders konusu olmanın ötesinde, birçok alanda karşımıza çıkan ve büyük öneme sahip bir konudur.
Çember hesaplama konusunda öğrendiğim bilgiler gerçekten faydalı oldu. Özellikle çemberin çevresinin ve yay uzunluğunun nasıl hesaplandığını anlamak, geometri derslerinde büyük bir avantaj sağladı. Örnek sorular üzerinden pratik yaparak bu konudaki becerimi geliştirebildim. Çember hesaplama, günlük hayatta da sıkça karşımıza çıkan bir durum.
Değerli İltiqaullah,
Yorumunuz için teşekkür ederim. Çember hesaplamanın geometri derslerinde sağladığı avantajları fark etmiş olmanız harika. Bu tür matematiksel bilgilerin günlük hayatta da kullanılması gerçekten önemli. Özellikle çevre ve yay uzunluğu hesaplamalarında pratik yaparak becerilerinizi geliştirmiş olmanız, konuyu daha iyi anlamanıza yardımcı olacaktır. Matematik, günlük yaşamda karşılaşılan birçok durum için temel bir yapı sağlar. Başarılarınızın devamını dilerim!
Çember çevre hesabı yaparken, pi sayısını kullanmanın ne kadar önemli olduğunu deneyimledim. Özellikle yarıçapı ve çapı doğru belirleyip formülde yerine koymak, doğru sonuçlar elde etmek için kritik. Peki, çember çevre hesabında pi sayısını nasıl kullanıyorsunuz?
Çember Çevresi Hesabı
Abdülala, çember çevresi hesabında pi sayısını kullanmanın önemine dikkat çekmişsiniz. Gerçekten de pi sayısı, çemberin temel özelliklerinden biridir ve çemberin çevresini hesaplarken kritik bir rol oynar. Çemberin çevresi, formül olarak C = 2πr veya C = πd şeklinde ifade edilir. Burada r yarıçapı, d ise çapı temsil eder.
Yarıçap ve Çapın Önemi
Yarıçapın ve çapın doğru bir şekilde belirlenmesi, hesaplamaların doğruluğu açısından büyük önem taşır. Yarıçapı doğru ölçmek, çevreyi hesaplamak için gereken temel bilgiyi sağlar. Aynı zamanda, çapı kullanarak çevreyi hesaplamak da mümkündür. Bu nedenle, her iki ölçümün de hassas bir şekilde alınması gerekir.
Pi Sayısının Rolü
Pi sayısı (π), çemberin çevresinin çapına oranıdır ve yaklaşık olarak 3.14 değerindedir. Bu sayı, çemberle ilgili birçok hesaplamada karşımıza çıkar ve matematiksel hesaplamaların temel taşlarından biridir. Pi sayısını kullanarak çember çevresini bulmak, matematiksel işlemlerin ve geometrik anlayışın gelişimi açısından da önemlidir.
Sonuç olarak, çember çevresi hesaplamalarında pi sayısını kullanmak, doğru sonuçlar elde etmek için vazgeçilmezdir. Yarıçap ve çapın doğru belirlenmesi, bu hesaplamaların temelini oluşturur.
Çemberin çap uzunluğunun nasıl bulunacağına dair örnekler ilginç. Ancak, çemberin çap uzunluğu nasıl bulunur? Yani yarıçapı kullanarak çemberin çapını hesaplamak için ne yapmalıyız? Bu konuda daha fazla bilgi alabilir miyim?
Dilrah,
Çemberin Çapı ve Yarıçapı
Çemberin çapı, çemberin ortasından geçen ve iki kenarını birleştiren en uzun doğru parçasıdır. Yarıçap ise çemberin merkezinden herhangi bir noktasına olan mesafedir. Yani, çemberin çapı, yarıçapın iki katına eşittir.
Çemberin Çapını Hesaplama
Eğer yarıçapı biliyorsanız, çemberin çapını hesaplamak oldukça basittir. Yarıçapı R olarak adlandıralım. Çemberin çapı D şu formülle bulunur:
D = 2 R
Örnek
Eğer bir çemberin yarıçapı 5 cm ise, çemberin çapı şöyle hesaplanır:
D = 2 5 cm = 10 cm
Yani çemberin çapı 10 cm olacaktır.
Eğer çemberin çevresini ya da alanını biliyorsanız, bu değerlerden de çapı bulabilirsiniz. Çemberin çevresi C = 2 π R formülü ile hesaplanır. Çevreyi biliyorsanız, çapı bulmak için şu şekilde işlem yapabilirsiniz:
D = C / π
Sonuç
Yarıçapı kullanarak çemberin çapını bulmak oldukça kolaydır. Yalnızca yarıçapı iki katına çıkarmanız yeterli. Bu temel bilgileri kullanarak çemberin ölçümleri hakkında daha fazla bilgi edinebilirsiniz.
Ãap uzunluğu verilmişse neden çemberin çevresini hesaplamak için yarıçap kullanmamız gerekiyor? Bu çapı kullanarak direkt çevreyi bulamaz mıyız?
Merhaba Tendubay,
Çap uzunluğu verildiğinde çemberin çevresini hesaplamak için yarıçapı kullanmamız gerektiğini düşünmek biraz kafa karıştırıcı olabilir. Ancak, aslında çapı doğrudan kullanarak çevreyi hesaplamak çok daha basittir. Çemberin çevresi formülü 2πr, yani 2 çarpı pi çarpı yarıçap. Çap, yarıçapın iki katı olduğundan, çapı kullanarak çevreyi hesaplamak için sadece πd (pi çarpı çap) formülünü kullanabilirsiniz. Yani, çapı doğrudan kullanarak çevreyi bulmak mümkündür ve bu aslında daha pratik bir yoldur.
Sevgiler,