
Koninin Hacim Formülü Nelerdir?
Koninin hacim formülü, geometri alanında önemli bir yere sahiptir. Bu formül, koninin taban yarıçapı ve yüksekliği kullanılarak hacmin hesaplanmasını sağlar. Matematiksel uygulamalarda ve mühendislikte sıkça kullanılmaktadır.
Koninin Hacim Formülü Nedir?Koniler, matematikte ve geometri alanında önemli bir şekil sınıfını temsil eder. Bir koni, bir dairesel tabana sahip olan ve bu tabanın merkezinden bir noktaya (apex veya tepe) doğru uzanan bir yüzeydir. Koninin hacmi ise, koninin içindeki üç boyutlu alanı ifade eder. Koninin hacim formülü, koninin taban yarıçapı ve yüksekliği ile doğrudan ilişkilidir. Koninin Hacim Formülü Koninin hacmi \( V \) aşağıdaki formül ile hesaplanır:\[ V = \frac{1}{3} \pi r^2 h \]Burada;- \( V \) : Koninin hacmi- \( \pi \) : Pi sayısı (yaklaşık 3.14159)- \( r \) : Koninin tabanının yarıçapı- \( h \) : Koninin yüksekliği Koninin Hacim Formülünün Bileşenleri Koninin hacim formülünü daha iyi anlamak için formülde yer alan bileşenlere daha ayrıntılı bir şekilde bakalım:
Koninin Hacmini Hesaplama Örneği Koninin hacmini hesaplamak için basit bir örnek üzerinden gidebiliriz. Diyelim ki bir koninin taban yarıçapı \( r = 3 \) cm ve yüksekliği \( h = 5 \) cm. Koninin hacmi hesaplanırken formülümüzü kullanarak:\[ V = \frac{1}{3} \pi (3)^2 (5) \]\[ V = \frac{1}{3} \pi (9) (5) \]\[ V = \frac{1}{3} \pi (45) \]\[ V = 15\pi \]Sonuç olarak, koninin hacmi yaklaşık olarak \( 47.12 \) cm³ olacaktır (yaklaşık \( \pi \) değeri kullanılarak). Koninin Hacmi ile İlgili Ekstra Bilgiler - Konilerin hacmi, mühendislik ve mimarlık gibi alanlarda sıkça kullanılır. Yapıların ve nesnelerin hacim hesaplamalarında koni formu göz önünde bulundurulabilir.- Ayrıca, konilerin hacmi, sıvı depolama kapları gibi pratik uygulamalarda da önemli bir rol oynar.- Koniler, matematiksel modelleme ve simülasyonlarda da yaygın olarak kullanılan geometrik şekillerdir. Sonuç Sonuç olarak, koninin hacim formülü, geometrik şekillerin hacimlerini hesaplamak için temel bir araçtır. Taban yarıçapı ve yükseklik gibi bileşenler, koninin hacmini belirlemede kritik bir öneme sahiptir. Bu formül, matematik ve mühendislik uygulamalarında geniş bir yelpazede kullanılmaktadır. Bu makale, koninin hacim formülünü ve bileşenlerini detaylı bir şekilde ele alarak, okuyucuların bu konuyu daha iyi anlamalarına yardımcı olmayı amaçlamaktadır. |
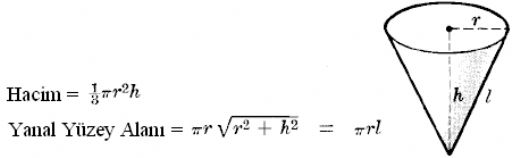















































Koni hacmi ve kesik koni hacmi hakkında çok faydalı bilgiler vermişsin. Özellikle konilerin türleri ve formülleri hakkında daha fazla bilgi sahibi olmak isteyenler için oldukça açıklayıcı. Kesik koninin hacim formülünü bulmakta zorlanıyordum, şimdi R ve r değerlerini kullanarak hesaplayabileceğimi anladım. Peki, bu formülleri günlük hayatta hangi pratik durumlarda kullanabiliriz? Örneğin, bir içecek kabının hacmini hesaplamak gibi bir durumda nasıl bir yol izleyebiliriz?
Öncelikle Teşekkürler Yağan, koni ve kesik koni hacimleri hakkında bilgi sahibi olman gerçekten güzel. Bu tür geometrik şekillerin formülleri, günlük hayatta pek çok durumda karşımıza çıkabiliyor.
Günlük Hayatta Kullanım Alanları
Örneğin, bir içecek kabının hacmini hesaplamak istediğinde, eğer kabın şekli bir koni veya kesik koni ise bu formülleri kullanarak hacmini bulabilirsin. İçinde ne kadar sıvı alabileceğini hesaplayarak, bir partide ya da etkinlikte ihtiyaç duyacağın içecek miktarını belirleyebilirsin.
Hacim Hesaplama Yöntemi
Bir içecek kabının hacmini hesaplamak için öncelikle kabın şekline karar vermen gerekiyor. Eğer kabın bir koni ise, hacim formülü V = (1/3) π r² h formülü ile uygulanabilir. Burada "r" tabanın yarıçapı, "h" ise yüksekliği temsil eder. Kesik koni için ise hacim formülü V = (1/3) π h (R² + Rr + r²) şeklindedir. Burada "R" üst tabanın yarıçapı, "r" alt tabanın yarıçapıdır ve "h" ise yüksekliği belirtir.
Pratik Örnek
Diyelim ki bir içecek kabın kesik koni şeklinde ve üst kısmının yarıçapı 3 cm, alt kısmının yarıçapı ise 5 cm ve yüksekliği 10 cm. Bu durumda hacmi hesaplamak için formülü kullanarak, içecek kabının ne kadar sıvı alabileceğini pratik bir şekilde bulabilirsin.
Bu tür hesaplamalar, hem iş yerinde hem de evde tasarruf sağlamak veya planlama yapmak için oldukça faydalı olabilir. Umarım bu bilgiler, koni ve kesik koni hacimlerinin günlük hayattaki pratik kullanımını daha iyi anlamana yardımcı olur!