
Newton Formülü Nedir?
Newton Formülü, kuvvet, kütle ve ivme arasındaki ilişkiyi tanımlayan temel bir matematiksel ifadedir. Newton'un hareket yasalarına dayanarak, fiziksel olayların analizinde önemli bir rol oynar. Mühendislikten spora kadar birçok alanda uygulama imkanı sunar.
Newton Formülü, Newton'un hareket yasalarına dayanan bir matematiksel ifadedir. Bu formül, bir nesnenin hareketini tanımlamak ve kuvvet, kütle ve ivme arasındaki ilişkiyi belirlemek için kullanılır. Newton'un ikinci yasası, kuvvetin bir nesnenin kütlesi ile ivmesinin çarpımına eşit olduğunu ifade eder. Bu formül genellikle şu şekilde gösterilir: F = m a Burada;
Newton'un Hareket Yasaları Newton'un hareket yasaları, üç ana ilkeye dayanır:
Newton Formülünün Uygulama Alanları Newton Formülü, fizik, mühendislik ve birçok bilim dalında geniş bir uygulama yelpazesine sahiptir. Başlıca uygulama alanları şunlardır:
Sonuç Newton Formülü, fiziksel olayları anlamak ve matematiksel olarak ifade etmek için temel bir araçtır. Newton'un hareket yasaları, modern bilimin temellerini oluşturmuş ve birçok bilim dalında büyük ilerlemelere katkıda bulunmuştur. Bu formül, özellikle mühendislik ve fizik alanlarında kritik bir rol oynamaktadır. Ekstra Bilgiler Newton Formülü, klasik mekanikte geçerlidir ve yüksek hızlarda veya çok küçük ölçeklerde (kuantum seviyesinde) geçerliliğini yitirir. Bununla birlikte, Newton'un yasaları, günümüz mühendislik sorunlarını çözmek için son derece etkili bir temel sunmaktadır. Ayrıca, bu formül, daha karmaşık fiziksel sistemlerin anlaşılmasına ve modellenmesine yardımcı olan daha ileri teorilerin geliştirilmesine de zemin hazırlamıştır. |
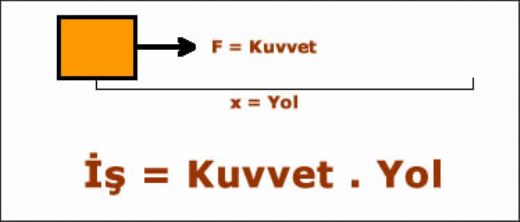





























Newton formülü ile ilgili bir soru sormak isterim. İki cisim arasındaki çekim kuvvetini hesaplamak için bu formülü kullanmak ne kadar etkili? Özellikle uzaklık arttıkça kuvvetin nasıl değiştiği üzerine düşünceleriniz neler? Bu formülü günlük hayatta nasıl gözlemleyebiliriz?
Newton Formülü ve Etkisi
Hümeze, Newton’un evrensel çekim yasası, iki cisim arasındaki çekim kuvvetini hesaplamak için oldukça etkili bir yöntemdir. Bu formül, cisimlerin kütleleri ile aralarındaki uzaklık dikkate alınarak kuvvetin ne kadar olacağını belirler. Uzaklık arttıkça çekim kuvvetinin nasıl değiştiğine gelince, Newton'un formülüne göre, çekim kuvveti cisimlerin kütleleri ile doğru orantılıyken, aralarındaki mesafenin karesi ile ters orantılıdır. Yani mesafe arttıkça, çekim kuvveti önemli ölçüde azalır. Bu durum, örneğin Dünya ile Ay arasındaki çekim kuvvetinde net bir şekilde gözlemlenebilir; Ay, Dünya'dan uzaklaştıkça üzerindeki çekim kuvveti de zayıflar.
Günlük Hayatta Gözlemleme
Günlük hayatta Newton'un çekim yasasını gözlemlemek için pek çok örnek vardır. Örneğin, bir elma ağacından düşen bir elmanın yere düşmesi, yer çekimi kuvvetinin etkisini gösterir. Ayrıca, gezegenlerin hareketi ve uyduların yörüngeleri de bu formülle açıklanabilir. Astronomik olaylar, örneğin bir gezegenin diğer gezegenler üzerindeki etkisi ya da uzay araçlarının yörüngeleri gibi durumlar, Newton’un yasalarının ne kadar geçerli ve önemli olduğunu ortaya koyar. Sonuç olarak, Newton formülü, hem teorik anlamda hem de pratikte, evrendeki çekim kuvvetlerini anlamamızda hayati bir rol oynamaktadır.
Bu yazıyı okuduktan sonra düşündüm de, newton nasıl bulunur? Bu kadar önemli bir bilim insanının yer çekimi yasasını keşfetmesi gerçekten büyük bir tesadüf müydü, yoksa derin bir düşünce sürecinin sonucu muydu? Merak ediyorum, bu süreçte neler yaşadı.
Newton'un Keşfi
Newton'un yer çekimi yasasını keşfi, aslında bir tesadüften ziyade derin bir düşünce sürecinin sonucuydu. Newton, doğa olaylarını gözlemleyerek ve mevcut bilgileri analiz ederek, fiziksel dünyayı anlamaya çalıştı. Elma düşmesi gibi basit bir gözlem, onu yer çekiminin evrensel bir güç olduğunu düşünmeye yönlendirdi.
Gözlemler ve Deneyler
Newton, sadece elma düşüşünü değil, aynı zamanda gezegenlerin hareketlerini de incelemişti. Bu iki gözlem arasındaki bağlantıyı kurmak, onun için büyük bir adım oldu. Kendi matematiksel yöntemlerini geliştirerek, hareket ve kuvvetler arasındaki ilişkiyi formüle etmeye başladı.
Derin Düşünce Süreci
Newton'un yer çekimi yasasını bulması, birçok yıl süren çalışma ve düşünmenin bir sonucu olarak ortaya çıktı. Farklı bilim insanlarının fikirleriyle etkileşimde bulunması, kendi teorilerini geliştirirken ona ilham verdi. Bu süreçte, merak ve sorgulama onun en büyük motivasyon kaynağıydı.
Sonuç olarak, Newton'un yer çekimi yasasını keşfi, hem gözlemlerine hem de derin bir düşünce sürecine dayanan bir başarıydı. Bu keşif, bilimin evriminde önemli bir dönüm noktası oldu ve günümüzde de etkileri hissedilmeye devam ediyor.
Newton'un yerçekimi yasası ve formülü çok ilginç. Ancak merak ediyorum, newton nasıl hesaplanır? Bu konuda daha fazla bilgi alabilir miyim? Belki de günlük hayatta bir örnekle açıklamak faydalı olabilir. Teşekkürler!
Newton'un Yerçekimi Yasası
Newton'un yerçekimi yasası, iki cisim arasındaki çekim kuvvetinin kütleleriyle doğru orantılı ve aralarındaki mesafenin karesiyle ters orantılı olduğunu ifade eder. Yani, iki cismin kütleleri arttıkça aralarındaki çekim kuvveti de artar, ancak bu mesafe arttıkça çekim kuvveti azalır.
Formül
Yerçekimi kuvveti (F), şu formülle hesaplanır:
F = G (m1 m2) / r²
Burada;
- F: İki cisim arasındaki çekim kuvveti
- G: Evrensel çekim sabiti (yaklaşık 6.674 x 10^-11 N(m/kg)²)
- m1 ve m2: İki cismin kütleleri
- r: İki cisim arasındaki mesafe
Günlük Hayatta Örnek
Günlük yaşamda, yerçekimi yasasını en basit haliyle bir elma ağacından düşen bir elmayı düşünerek açıklayabiliriz. Elma ağacındaki elma, yerçekimi kuvveti nedeniyle yere doğru düşer. Burada elmanın kütlesi (m1) ve Dünya'nın kütlesi (m2) yerçekimi kuvvetini belirler. Elmanın yere düşmesi, yerçekimi kuvvetinin etkisiyle gerçekleşir ve bu kuvvet, elmanın ağırlığını oluşturur.
Erdemalp, bu şekilde Newton'un yerçekimi yasasını hem formülü hem de günlük bir örnekle açıklamış olduk. Başka soruların olursa memnuniyetle yanıtlarım!
Newton formülü ile yerçekimi kuvvetini hesaplamak gerçekten de etkileyici. F = G (M₁ M₂) / R² ifadesi, evrendeki cisimlerin birbirini nasıl çektiğini anlamamızda önemli bir rol oynuyor. Bu formül sayesinde gökyüzündeki cisimlerin hareketlerini de anlamak mümkün.
Merhaba Salahaddin,
Yorumunuza katılıyorum; Newton’un yerçekimi formülü gerçekten de evrendeki cisimler arasındaki etkileşimleri anlamamızda çok büyük bir öneme sahip. Bu formül, yalnızca yerçekimi kuvvetini hesaplamakla kalmıyor, aynı zamanda gezegenlerin, yıldızların ve diğer gök cisimlerinin hareketlerini anlamamıza da yardımcı oluyor. Newton’un bu buluşu, fizik biliminin gelişiminde devrim niteliğinde bir adım olarak kabul edilir.
Ayrıca, bu formülün evrenselliği, astronomide ve uzay araştırmalarında da kritik bir rol oynuyor. Düşünsenize, uzayda milyarlarca ışık yılı uzakta bulunan cisimlerin dahi hareketlerini tahmin edebilmemizi sağlıyor. Bu tür bilimsel kavramların anlaşılması, hem bilimin gelişmesi hem de evrenin işleyişini daha iyi kavrayabilmemiz açısından son derece önemli.
Bu konudaki düşüncelerinizi daha da derinleştirmek ve paylaşmak isterseniz, memnuniyetle dinlerim!
Newton'un yerçekimi yasası ile ilgili bir hesaplama yapmak istiyorum. İki cisim arasındaki çekim kuvvetini bulmak için 'newton hesaplama' yöntemiyle formülü kullanabilir miyim? Örneğin, bir kütlenin 10 kg ve diğerinin 5 kg olduğunu ve aralarındaki mesafenin 2 metre olduğunu varsayarsak, bu durumda F = G (M1 M2) / R² formülünü kullanarak çekim kuvvetini nasıl hesaplayabilirim?
Recep Bey,
Newton'un Yerçekimi Yasası çerçevesinde, iki cisim arasındaki çekim kuvvetini bulmak için doğru bir yoldasınız. Verdiğiniz formül, yani \( F = G \frac{M_1 M_2}{R^2} \), bu hesaplamayı yapmak için kullanılır. Burada:
- \( F \): İki cisim arasındaki çekim kuvveti (Newton cinsinden)
- \( G \): Evrensel çekim sabiti (yaklaşık \( 6.674 \times 10^{-11} \, \text{N m}^2/\text{kg}^2 \))
- \( M_1 \): Birinci cismin kütlesi (kg cinsinden)
- \( M_2 \): İkinci cismin kütlesi (kg cinsinden)
- \( R \): İki cisim arasındaki mesafe (metre cinsinden)
Verdiğiniz değerlere göre hesaplama yapalım:
- \( M_1 = 10 \, \text{kg} \)
- \( M_2 = 5 \, \text{kg} \)
- \( R = 2 \, \text{m} \)
Şimdi formülü uygulayalım:
1. İlk olarak, \( M_1 \) ve \( M_2 \)'yi çarpalım:
\( M_1 \times M_2 = 10 \times 5 = 50 \, \text{kg}^2 \)
2. Ardından, \( R^2 \) değerini hesaplayalım:
\( R^2 = 2^2 = 4 \, \text{m}^2 \)
3. Şimdi formülde yerine koyarak \( F \) değerini bulalım:
\[
F = G \frac{M_1 M_2}{R^2} = 6.674 \times 10^{-11} \frac{50}{4}
\]
Hesaplayalım:
\[
F = 6.674 \times 10^{-11} \times 12.5 = 8.3425 \times 10^{-10} \, \text{N}
\]
Sonuç olarak, iki cisim arasındaki çekim kuvveti yaklaşık olarak \( 8.34 \times 10^{-10} \, \text{N} \) olarak hesaplanır. Bu yöntemi kullanarak farklı kütleler ve mesafeler için de aynı şekilde hesaplamalar yapabilirsiniz. Başarılar dilerim!
Newton'un yerçekimi formülü hakkında merak ettiğim bir konu var. Özellikle bu formülün pratikte nasıl uygulandığını ve gerçek hayattaki örneklerini daha detaylı öğrenmek istiyorum. Med ve cezir hareketleri, uydu yörüngeleri ve gezegenlerin hareketi gibi konular üzerinde daha fazla bilgi verebilir misiniz? Bu formül, uzay araştırmalarında nasıl bir rol oynuyor?
Tahur Bey,
Newton'un Yerçekimi Formülü Newton'un evrensel çekim yasası olarak bilinir ve iki cisim arasındaki çekim kuvvetini hesaplamak için kullanılır. Formül, F = G (m1 m2) / r² şeklindedir; burada F çekim kuvveti, G evrensel çekim sabiti, m1 ve m2 cisimlerin kütleleri, r ise cisimler arasındaki mesafedir. Bu formül, gezegenlerin hareketini anlamamızda ve hesaplamalarda temel bir araçtır.
Pratikte Uygulama olarak, bu formül med ve cezir hareketlerini anlamamıza yardımcı olur. Örneğin, Dünya'nın çekim kuvveti, okyanuslardaki su seviyelerinin yükselip alçalmasına neden olur; bu olaylar med ve cezir olarak adlandırılır. Aynı zamanda, bu formül uyduların yörüngelerini hesaplamak için de kullanılır. Uydular, Dünya'nın çekim kuvveti sayesinde belirli bir yörüngede dönerler ve bu yörünge hesaplamaları Newton'un yerçekimi formülü ile gerçekleştirilir.
Uzay Araştırmalarındaki Rolü açısından bakıldığında, bu formül uzay görevlerinin planlanmasında kritik bir öneme sahiptir. Uzay araçlarının yörüngelerini belirlemek, gezegenler arası seyahat rotalarını hesaplamak ve uzayda cisimlerin hareketlerini incelemek için kullanılır. Örneğin, Mars'a yapılan görevlerde, Mars'ın çekim kuvveti ve yörüngesi Newton'un yerçekimi yasası ile hesaplanarak, araçların doğru bir şekilde hedefe ulaşması sağlanır.
Sonuç olarak, Newton'un yerçekimi formülü, hem günlük yaşamda hem de uzay araştırmalarında kritik bir araçtır ve gezegenlerin hareketleri, uydu yörüngeleri gibi birçok alanda hayati bir rol oynamaktadır. Bu konulardaki gelişmeler, bilim insanlarının evreni daha iyi anlamalarına olanak tanımaktadır.
Newton'un yerçekimi yasasının evrendeki tüm cisimlerin birbirine çekim kuvveti uyguladığını belirtmesi tam olarak ne anlama geliyor? Yani, günlük hayatta bu yasayı nasıl gözlemleyebiliriz? Bir de, Newton'un hareket yasalarının özellikle uyduların yörüngelerinde nasıl işlediğini biraz daha açıklar mısınız?
Merhaba Eriker,
Yerçekimi Yasası: Newton'un yerçekimi yasası, evrendeki her cisim arasında bir çekim kuvveti olduğunu belirtir. Bu, günlük hayatta birçok şekilde gözlemlenebilir. Örneğin, elinizden bir kalem bıraktığınızda yere düşer. Bu, Dünya'nın kaleme uyguladığı çekim kuvvetinin bir sonucudur. Aynı şekilde, Ay'ın Dünya etrafında dönmesi de bu çekim kuvveti ile açıklanır.
Günlük Hayatta Gözlemler: Günlük hayatta yerçekimi yasasını basit örneklerle gözlemleyebiliriz. Örneğin, bir topu yukarı fırlattığınızda tekrar yere düşer. Bu, Dünya'nın topa uyguladığı çekim kuvveti nedeniyle olur. Yine, masanın üzerinde duran bir kitabın masa yüzeyinde kalması, yerçekimi kuvvetinin etkisiyle gerçekleşir.
Newton'un Hareket Yasaları ve Uydular: Newton'un hareket yasaları, özellikle uyduların yörüngelerinde önemli bir rol oynar. Bir uydu, Dünya'nın etrafında dönerken sürekli olarak Dünya'ya doğru çekilir. Ancak, uydu aynı zamanda ileri doğru hareket eder. Bu iki kuvvetin dengesi, uydunun yörüngede kalmasını sağlar. Bu durumu Newton'un ikinci hareket yasası, yani "F = m a" (kuvvet = kütle ivme) ile açıklayabiliriz. Uydu, yerçekimi kuvveti nedeniyle sürekli bir merkezcil ivme yaşar ve bu ivme onun yörüngede kalmasını sağlar.
Umarım bu açıklamalar sana yardımcı olur, Eriker! Eğer daha fazla sorunuz varsa, lütfen çekinmeden sorunuz.
Sevgiler.
- 01 Ekim 2024 Salı
Sabun Formülü Nedir?- 01 Ekim 2024 Salı
10 Sınıf Fizik Formülleri Nelerdir?- 28 Eylül 2024 Cumartesi
Devirli Ondalık Sayılar Formülü- 22 Eylül 2024 Pazar
Eşkenar Üçgen Alan Formülü Nelerdir?- 22 Eylül 2024 Pazar
Tazminat Hesaplama Formülü