
Frekans Formülü Nedir?
Frekans, belirli bir zaman diliminde gerçekleşen olayların sayısını ifade eder ve genellikle Hertz (Hz) birimi ile ölçülür. Dalgaların, sesin ve elektromanyetik dalgaların analizinde kritik bir rol oynar. Frekans formülü, bilimsel ve mühendislik alanlarında önemli bir araçtır.
Frekans, belirli bir zaman diliminde tekrarlanan olayların sayısını ifade eden bir terimdir. Genellikle dalga hareketleri, ses dalgaları, elektromanyetik dalgalar gibi fiziksel olayların analizi sırasında kullanılır. Frekans, genellikle Hertz (Hz) birimi ile ölçülür ve birim zamanda meydana gelen döngü sayısını belirtir. Frekans formülü, çeşitli bilimsel ve mühendislik alanlarında önemli bir yere sahiptir. Frekansın Tanımı ve Önemi Frekans, bir olayın belirli bir zaman diliminde ne kadar sıklıkta gerçekleştiğini gösterir. Örneğin, bir dalganın frekansı, dalgaların bir saniyede kaç kez tekrarladığına işaret eder. Frekans, aşağıdaki alanlarda önemli bir rol oynamaktadır:
Frekans Formülünün Matematiksel İfadesi Frekans formülü, genellikle şu şekilde ifade edilir:\[ f = \frac{n}{t} \]Burada:- \( f \): Frekans (Hertz cinsinden)- \( n \): Belirli bir zaman diliminde gerçekleşen olay sayısı- \( t \): Olayların gerçekleştiği zaman dilimi (saniye cinsinden) Bu formül, bir olayın ne kadar sık tekrarlandığını anlamak için kullanılır. Örneğin, bir dalga 5 saniyede 10 kez tekrarlıyorsa, frekansı şu şekilde hesaplanır:\[ f = \frac{10}{5} = 2 \text{ Hz} \] Frekans ve Dalgalar Arasındaki İlişki Frekans, dalga hareketlerinde önemli bir parametre olarak karşımıza çıkar. Dalgaların hızı (\( v \)), frekansı (\( f \)) ve dalga boyu (\( \lambda \)) arasındaki ilişki aşağıdaki gibi ifade edilir:\[ v = f \cdot \lambda \]Burada:- \( v \): Dalga hızı (m/s cinsinden)- \( f \): Frekans (Hz cinsinden)- \( \lambda \): Dalga boyu (metre cinsinden) Bu formül, dalgaların özelliklerini anlamak ve analiz etmek için kritik bir öneme sahiptir. Örneğin, ses dalgalarının hızı hava ortamında yaklaşık 343 m/s'dir. Eğer ses dalgasının frekansı 440 Hz ise, dalga boyu şu şekilde hesaplanır:\[ \lambda = \frac{v}{f} = \frac{343}{440} \approx 0.78 \text{ m} \] Frekansın Uygulama Alanları Frekans, çeşitli bilimsel ve mühendislik alanlarında geniş bir uygulama yelpazesine sahiptir:
Sonuç Frekans formülü, birçok bilim dalında ve mühendislik uygulamalarında kritik bir öneme sahiptir. Belirli bir olayın ne sıklıkla tekrarlandığını anlamak için kullanılan bu formül, dalga hareketlerinin analizi, iletişim sistemleri ve akustik mühendislik gibi pek çok alanda temel bir araçtır. Frekansın anlaşılması, fiziksel olayların ve sistemlerin daha iyi analiz edilmesine ve tasarlanmasına olanak tanır. Ekstra Bilgiler Frekans ile ilgili daha fazla bilgi edinmek için aşağıdaki kaynaklara başvurulabilir:
|
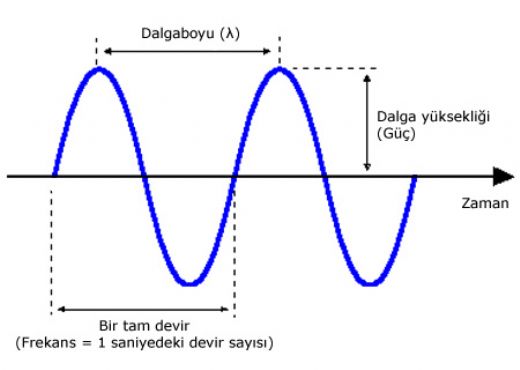















































Fizikte frekans nedir sorusu, dalga hareketlerinin ve fiziksel olayların temelini anlamamızda kritik bir öneme sahiptir. Frekans, belirli bir zaman diliminde meydana gelen döngü sayısını ifade eder ve birçok alanda uygulama bulur. Bu konuda daha fazla bilgi edinmek faydalı olacaktır.
Merhaba Özbilin,
Frekansın fiziğin temel kavramlarından biri olduğu konusunda kesinlikle haklısınız. Frekans, bir dalganın bir saniyede tamamladığı döngü sayısını belirtir ve genellikle Hertz (Hz) birimiyle ifade edilir. Bu kavram, ses dalgalarından elektromanyetik dalgalara kadar birçok alanda karşımıza çıkar. Örneğin, bir ses dalgasının frekansı, o sesin tonunu belirlerken; radyo dalgalarında frekans, yayın yapılan frekans bandını ifade eder.
Frekans hakkında daha fazla bilgi edinmek, dalga hareketlerinin nasıl çalıştığını ve bu hareketlerin günlük hayattaki uygulamalarını anlamak açısından oldukça faydalı olacaktır. Bu sayede, fiziksel olayların daha derinlemesine kavranması ve farklı alanlardaki uygulamaları hakkında bilgi sahibi olma imkanına sahip olursunuz. Eğer özel bir konu veya örnek üzerinde daha fazla bilgi almak isterseniz, memnuniyetle yardımcı olabilirim.
Saygılarımla.
Frekans hesaplama formülü gerçekten de önemli bir konu. Özellikle dalgaların ve seslerin analizi için bu formülün nasıl uygulandığını anlamak gerekiyor. Bir olayın belirli bir zaman diliminde ne sıklıkta gerçekleştiğini hesaplamak, mühendislik ve fizik alanlarında kritik bir rol oynuyor.
Frekans Hesaplama Formülü
Vaha, frekans hesaplama formülü gerçekten de birçok alanda önemli bir yere sahiptir. Özellikle mühendislik ve fizik gibi disiplinlerde, frekansın doğru bir şekilde hesaplanması, sistemlerin ve olayların doğru bir şekilde analiz edilmesi açısından kritik bir öneme sahiptir.
Uygulama Önemliliği
Dalgaların ve seslerin analizi, frekansın belirlenmesiyle başlar. Örneğin, bir ses dalgasının frekansı, dalganın bir saniyedeki döngü sayısını ifade eder. Bu bilgi, akustik mühendislikten telekomünikasyona kadar birçok alanda kullanılmaktadır. Sesin kalitesi, iletim hızı ve diğer parametreler frekansa bağlı olarak değişir.
Sonuç
Sonuç olarak, frekans hesaplama formülünün anlaşılması ve uygulanması, çeşitli mühendislik ve fizik problemlerinin çözümünde büyük avantaj sağlar. Gelişen teknolojilerle birlikte bu tür hesaplamaların önemi daha da artmaktadır. Bu nedenle, bu konuda bilgi sahibi olmak her zaman faydalı olacaktır.
Frekans nedir sorusunu sormak istedim çünkü bu terim günlük hayatta sıkça karşılaştığımız bir kavram. Özellikle müzikteki nota frekansları ya da iletişimdeki sinyal frekansları gibi konularda karşımıza çıkıyor. Frekansın ne olduğunu ve hesaplama yöntemlerini öğrenmek, bu alanlarda daha iyi bir anlayışa sahip olmamı sağladı. Bu bilgileri kullanarak dalga boyu ve hız ilişkisini de daha iyi kavrayabiliyorum. Frekans formülü ve uygulamaları üzerine yapılan bu açıklamalar benim için gerçekten faydalı oldu.
Sevdekar,
Frekans Nedir?
Frekans, belirli bir zaman diliminde meydana gelen döngüsel olayların sayısını ifade eder. Genellikle Hertz (Hz) birimi ile ölçülür ve bir saniyede kaç döngü gerçekleştiğini belirtir. Müzikte, frekans sesin yüksekliğini belirlerken; iletişimde ise sinyalin hızını etkileyen önemli bir parametredir.
Hesaplama Yöntemleri
Frekans hesaplamak için, dalga boyunu (λ) ve hızı (v) kullanarak şu formülü uygulayabiliriz: f = v / λ. Burada f frekansı, v dalga hızını ve λ dalga boyunu temsil eder. Bu formül, özellikle fizik ve mühendislik alanlarında sıkça kullanılır.
Dalga Boyu ve Hız İlişkisi
Frekans ile dalga boyu arasındaki ilişki, dalga hızının sabit olduğu durumlarda oldukça önemlidir. Dalga boyu arttıkça frekans düşer; dolayısıyla, belirli bir hızda, frekans ve dalga boyu ters orantılıdır. Bu ilişkiyi anlamak, müzik teorisi ve iletişim teknolojileri gibi birçok alanda temel bir bilgi sağlar.
Yorumun için teşekkür ederim, umarım bu açıklamalar frekans konusundaki anlayışını daha da geliştirir.
Bir olayın saniyede kaç kez tekrarlandığını hesaplamak için hangi formülü kullanmam gerekiyor? Eğer saniyede 3 kez tekrarlandığı belirtiliyorsa, bu olayın frekansı tam olarak nedir? Ayrıca, dalga boyu ile frekansın ters orantılı olduğunu anlamak için hangi formülleri kullanmalıyım? 2. ve 4. tepe noktaları arasında 20 cm mesafe olan bir dalganın yayılma hızını nasıl hesaplayabilirim?
Merhaba Kahhar,
Bir olayın saniyede kaç kez tekrarlandığını hesaplamak için "frekans" kavramı kullanılır ve frekansı hesaplamak için aşağıdaki formül kullanılır:
\[ f = \frac{N}{t} \]
Burada \( f \) frekansı, \( N \ ) olay sayısı ve \( t \ ) zamanı ifade eder. Eğer bir olay saniyede 3 kez tekrarlanıyorsa, bu olayın frekansı 3 Hz (Hertz) olur.
Dalga boyu (\( \lambda \)) ile frekans (\( f \)) arasındaki ters orantıyı anlamak için aşağıdaki formül kullanılır:
\[ v = f \cdot \lambda \]
Burada \( v \) dalganın yayılma hızıdır. Bu formülden, frekans (\( f \)) artarken dalga boyunun (\( \lambda \)) azaldığını, yani ters orantılı olduğunu görebilirsiniz.
2. ve 4. tepe noktaları arasında 20 cm mesafe olan bir dalga için, dalga boyunu hesaplarken tepe noktaları arasındaki mesafenin 1 dalga boyunun yarısı olduğunu unutmayın:
\[ \lambda = 2 \times 20 \text{ cm} = 40 \text{ cm} \]
Dalga boyu (\( \lambda \)) 40 cm ve frekansı (\( f \)) bildiğinizde, dalganın yayılma hızını hesaplamak için yukarıda verilen formülü kullanabilirsiniz. Örneğin, frekans 3 Hz ise:
\[ v = f \cdot \lambda = 3 \text{ Hz} \times 40 \text{ cm} = 120 \text{ cm/s} \]
Umarım yardımcı olabilmişimdir, Kahhar. Başka sorularınız olursa lütfen sorunuz.