Köklü Sayılar Formülleri Nelerdir?

Kök sayıları, matematikte önemli bir yere sahiptir ve sayıların belirli bir dereceden kökünü ifade eder. Karekök ve küpkök gibi çeşitleri vardır. Bu sayılar, matematiksel işlemler ve denklemlerin çözümünde kritik bir rol oynar, ayrıca mühendislik ve fizik gibi alanlarda da sıkça kullanılır.

Konu kakkında 1 soru soruldu ve cevaplandı

Kökler ve Kök Sayıları Üzerine Genel Bilgi

Kök sayıları, matematikte bir sayının belirli bir dereceden kökünü ifade eder. Genellikle karekök, küpkök gibi terimler kullanılır. Kökler, bir sayı kümesindeki elemanların belirli bir yapı içerisinde nasıl bir araya geldiğini anlamamıza yardımcı olur. Köklerin temel özellikleri ve formülleri, matematiksel işlemler ve denklemler üzerinde önemli bir rol oynar.

Kök Sayıları ve Tanımları

Kök sayıları, genellikle "√" sembolüyle gösterilir. Kökler, genellikle aşağıdaki gibi tanımlanır:

Kare Kök: Bir sayının karekökü, o sayının kendisi ile çarpıldığında orijinal sayıyı veren bir sayıdır. Örneğin, √9 = 3 çünkü 3 x 3 = 9.
Küpkök: Bir sayının küpkökü, o sayının kendisi ile üç kez çarpıldığında orijinal sayıyı veren bir sayıdır. Örneğin, ∛27 = 3 çünkü 3 x 3 x 3 = 27.
Genel Kök: n. dereceden kök, a sayısının n. dereceden kökü, n x n x n... şeklinde n kez çarpıldığında a sayısını veren bir sayıdır ve matematiksel olarak √[n]{a} ile gösterilir.

Kök Sayılarının Temel Özellikleri

Kök sayılarının bazı temel özellikleri şunlardır:

√(a b) = √a √b: İki sayının çarpımının kökü, bu sayıların köklerinin çarpımına eşittir.
√(a / b) = √a / √b: İki sayının bölümünün kökü, bu sayıların köklerinin bölümüne eşittir.
(√a)² = a: Bir kökün karesi, kök altındaki sayıya eşittir.
√(a²) = |a|: Bir sayının karesinin kökü, sayının mutlak değerine eşittir.

Kök Sayıları ile İlgili Önemli Formüller

Kök sayıları ile ilgili bazı önemli formüller şunlardır:

√(a+b) ≠ √a + √b: Köklerin içindeki sayıların toplamının kökü, köklerin toplamına eşit değildir.
(√a + √b)² = a + b + 2√(ab): İki kökün toplamının karesi, bu köklerin karesinin toplamı ile iki kat köklerin çarpımının toplamına eşittir.
(√a - √b)² = a + b - 2√(ab): İki kökün farkının karesi, bu köklerin karesinin toplamı ile iki kat köklerin çarpımının farkına eşittir.
√(a - b) ≠ √a - √b: Köklerin içindeki sayıların farkının kökü, köklerin farkına eşit değildir.

Kök Sayıları ile Çözümleme

Kök sayıları, matematiksel problem çözme süreçlerinde önemli bir yer tutar. Özellikle denklemleri çözmek için kökler sıkça kullanılır. Örneğin, aşağıdaki denklemi ele alalım:√x + 5 = 9Bu denklemi çözmek için her iki taraftan 5 çıkararak başlarız:√x = 4Sonrasında her iki tarafın karesini alarak x değerini bulabiliriz: x = 16

Kök Sayıları ve Uygulamaları

Kök sayılarının matematiksel anlamı dışında çeşitli uygulamaları bulunmaktadır. Özellikle mühendislik, fizik ve istatistik gibi alanlarda kök sayıları sıklıkla kullanılmaktadır. Örneğin, fiziksel hesaplamalarda alan ve hacim hesaplamaları için kök sayıları kullanılarak ölçümler yapılabilir.

Sonuç

Kök sayıları ve bunların formülleri, matematiksel düşünme becerilerinin geliştirilmesinde önemli bir rol oynamaktadır. Köklerin temel özellikleri ve uygulamaları, matematiksel problemlerin çözümünde ve çeşitli bilimsel alanlarda önemli bir yer tutmaktadır. Kök sayıları hakkında derinlemesine bilgi sahibi olmak, öğrencilerin matematiksel anlayışlarını ve problem çözme yeteneklerini artıracaktır.

Yeni Soru Sor / Yorum Yap

Sizden Gelen Sorular / Yorumlar

Arsu 12 Ağustos 2024 Pazartesi

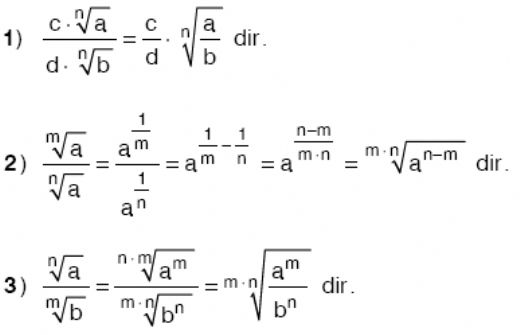
Köklü sayılarla ilgili bu bilgiler gerçekten çok faydalı. Özellikle toplama ve çıkarma işlemlerinin nasıl yapıldığına dair açıklamalar dikkatimi çekti. Kök derecelerinin ve kökün içindeki sayıların aynı olması gerektiği gerçeği, birçok kişi için kafa karıştırıcı olabilir. Bu kuralların uygulanması gerektiği durumları yaşadığınızda nasıl bir yol izlediniz? Köklerin içindeki ifadeleri eşit hale getirmek için kullandığınız yöntemler var mı?

Admin 12 Ağustos 2024 Pazartesi

Merhaba Arsu,

Köklü sayılarla ilgili düşünceleriniz için teşekkür ederim. Toplama ve Çıkarma İşlemleri konusundaki açıklamaların faydalı olduğunu duymak güzel. Genellikle köklerin içinde bulunan sayıların eşitlenmesi, karmaşık görünebilir, ancak bazı yöntemlerle bu durumu kolayca aşabiliriz.

Köklerin Eşitlenmesi için en yaygın yöntemlerden biri, köklerin içindeki sayıları aynı hale getirmektir. Örneğin, √2 ve √8 ile işlem yaparken, √8'i √(42) şeklinde yazarak √4 ve √2'yi ayrı ayrı ele alabiliriz. Buradan √4'ün 2 olduğunu biliyoruz, dolayısıyla işlemimizi kolaylaştırmış oluyoruz.

Ayrıca, Rasyonel Sayılarla İşlem Yapma yöntemi de oldukça etkilidir. Kök dışındaki sayıları rasyonel hale getirerek işlem yapmak, hesabı daha anlaşılır hale getirebilir. Özellikle köklerin derecelerinin eşitlenmesi gerektiği durumlarda bu yöntem oldukça kullanışlıdır.

Bu tarz durumları yaşadığınızda, genellikle hangi yöntemin işleme en uygun olduğunu değerlendirip uygulamak en iyisi. Deneyerek ve pratik yaparak bu tür işlemleri daha iyi anlamak mümkün. Sizin bu konudaki deneyimlerinizi merak ediyorum, nasıl bir yol izlediniz?

Sevgiler,