
Silindir Hacim Formülü Nedir?
Silindirin hacmi, mühendislik ve bilim alanlarında önemli bir kavramdır. Hacim hesaplama formülü, silindirin taban alanı ile yüksekliğinin çarpımıyla elde edilir. Bu bilgi, çeşitli pratik uygulamalarda kritik bir rol oynar ve silindirik yapıların tasarımında kullanılır.
Silindir, matematik ve mühendislik alanlarında sıkça karşılaşılan bir üç boyutlu geometrik şekildir. Silindirin hacmi, silindirin iç kısmının kapladığı alanı ifade eder ve bu hacim hesaplaması, çeşitli mühendislik uygulamaları ve fiziksel hesaplamalar için önemlidir. Silindirin hacmini hesaplamak için kullanılan formül, silindirin taban alanı ile yüksekliğinin çarpımı ile elde edilir. Silindirin Temel Özellikleri Silindirin bazı temel özellikleri şunlardır:
Silindir Hacim Formülü Silindirin hacmini hesaplamak için kullanılan formül şu şekildedir:\[V = \pi r^2 h\]Burada:
Hacim Hesaplaması Örneği Bir silindirin hacmini hesaplamak için örnek bir durum ele alalım. Diyelim ki, silindirin tabanının yarıçapı 5 cm ve yüksekliği 10 cm olsun. Bu durumda hacim hesaplaması şu şekilde yapılır:\[V = \pi r^2 h = \pi (5)^2 (10) = \pi (25) (10) = 250\pi \approx 785.4 \, cm^3\]Bu hesaplama, silindirin hacminin yaklaşık 785.4 santimetreküp olduğunu göstermektedir. Silindir Hacmi Uygulamaları Silindirin hacmi, çeşitli alanlarda önemli uygulamalara sahiptir. Bunlar arasında:
Sonuç Sonuç olarak, silindirin hacim formülü, mühendislik ve bilim alanlarında önemli bir yere sahiptir. Silindirin hacmini hesaplamak, çeşitli uygulamalarda kullanılabilen kritik bir bilgidir. Elde edilen hacim değerleri, tasarım ve analiz süreçlerinde önemli rol oynamaktadır. Silindirin hacim hesaplaması, yalnızca matematiksel bir işlem değil, aynı zamanda pratik uygulamalara dönük bir bilgi setidir. Ek bilgi olarak, silindirin hacmini etkileyen faktörler arasında malzeme yoğunluğu, sıcaklık değişimleri ve silindirin içeriği de yer alır. Bu faktörler, silindirin gerçek hayattaki uygulamalarında önemli sonuçlar doğurabilir. |
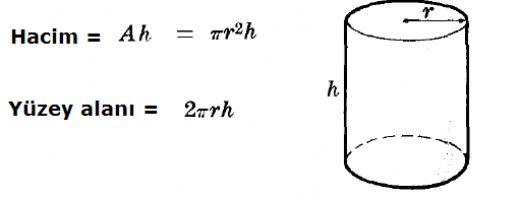





























Silindirin taban alanı nasıl bulunur? Silindirin tabanı daire şeklindedir ve taban alanı hesaplamak için dairenin alan formülünü kullanmalıyız. Yani, A = πr² formülünü uygulayarak, yarıçapı bildiğimizde taban alanını kolayca bulabiliriz. Bu hesaplama, hacim bulma işlemlerinde de önemlidir.
Kiram,
Silindirin Taban Alanı Hesaplama
Silindirin taban alanını bulmak için dairenin alan formülünü kullanmak gerçekten de doğru bir yaklaşım. Daire, silindirin tabanı olduğu için, taban alanı A = πr² formülü ile hesaplanır. Burada r, dairenin yarıçapıdır.
Yarıçapın Önemi
Yarıçapı bildiğimizde, taban alanını kolayca hesaplayabiliriz. Bu, silindirin hacmini bulmak için de kritik bir adımdır. Hacim hesaplamasında taban alanını yüksekliğe çarparak sonuca ulaşırız (V = A h).
Uygulama Örneği
Örneğin, yarıçapı 3 cm olan bir silindirin taban alanını hesaplayalım:
A = π (3 cm)² = π 9 cm² ≈ 28.27 cm².
Bu şekilde, silindirin taban alanını belirleyerek, hacim hesaplamalarımızda kullanabiliriz.
Bu bilgilerle silindirin taban alanını bulma işleminin ne kadar kolay olduğunu görebilirsin. Başka bir konuda yardımcı olmamı ister misin?
Silindir hacim formülleri ile ilgili bilgileri okudum. Silindirin hacmini hesaplamak için kullanılan formül, mühendislik ve fizik uygulamalarında önemli bir yere sahip. Özellikle silindirin taban alanını ve yüksekliğini göz önünde bulundurarak hesaplama yapmak, pratikte büyük fayda sağlıyor.
Sayın Uluberk,
Silindir Hacmi Hesaplaması konusunda yaptığınız değerlendirme oldukça yerinde. Silindirin hacmi, mühendislik ve fizik alanında birçok uygulama için kritik öneme sahiptir. Bu hesaplama, özellikle su depolama tankları, boru hatları ve diğer silindirik yapılar söz konusu olduğunda pratikte büyük fayda sağlamaktadır.
Formül ve Uygulama açısından, silindirin hacmini hesaplamak için kullanılan formül V = πr²h şeklindedir. Burada r silindirin taban yarıçapı, h ise yüksekliğidir. Bu formül, silindirik nesnelerin hacimlerinin hızlı bir şekilde hesaplanmasına olanak tanır.
Ayrıca, Günlük Hayatta Kullanımı açısından, bu bilgilerin pek çok alanda uygulandığını görebiliriz. Örneğin, içecek endüstrisinde şişe hacimlerini belirlemek ya da inşaat mühendisliğinde silindirik kolonların hacimlerini hesaplamak için bu formüller sıklıkla kullanılmaktadır.
Bu tür konulara ilginiz ve yaptığınız araştırmalar için sizi tebrik ediyorum. Daha fazla bilgi edinmek veya tartışmak isterseniz, her zaman buradayım!
Silindirin hacmini hesaplamak için taban alanını bulmak önemli. Taban alanı formülü ile başlayarak, yüksekliği ile çarptığımızda hacmi elde ediyoruz. Örneklerde verilen değerler, silindir alan hacim hesaplamalarının ne kadar kolay olduğunu gösteriyor. Bu yöntemle pratik yaparak daha iyi anlayabiliriz.
Merhaba Erçin,
Silindirin hacmini hesaplamak için taban alanının önemini vurgulaman çok doğru. Taban alanı, silindirin dairesel tabanının alanını ifade eder ve bu alanı bulmak için genellikle πr² formülü kullanılır. Burada r, silindirin yarıçapıdır. Daha sonra bu taban alanını silindirin yüksekliği ile çarparak hacmi buluyoruz. Hacim formülü ise V = πr²h şeklindedir.
Verdiğin örneklerin, bu hesaplamaların ne kadar kolay yapılabileceğini göstermesi de çok faydalı. Pratik yaparak bu formülleri daha iyi kavrayabilir ve farklı boyutlardaki silindirlerin hacimlerini hızlıca hesaplayabilirsin. Matematiksel işlemlerde pratik gerçekten önemlidir. Bu konuda daha fazla sorunuz olursa, yardımcı olmaktan memnuniyet duyarım.
İyi çalışmalar!
Silindir hacmi hesaplamak için silindir formülü oldukça önemli. Verilen örneklerde silindirin hacmini bulmak için taban alanı ile yükseklik çarpılıyor. Özellikle yarıçap ve yüksekliği aynı birim cinsinden kullanmak, sonucu doğru elde etmek için kritik. Bu formülü iyi anlamak gerek.
Merhaba Erzan,
Silindir hacmi hesaplama konusuna değindiğin için teşekkürler. Gerçekten de silindirin hacmini bulmak için kullanılan formül oldukça basit ama etkili. Hacim hesaplama işlemi, taban alanı ile yükseklik çarpılarak elde ediliyor. Taban alanı, dairenin alanı olduğu için, yarıçapın karesi ile π sayısını çarpmamız gerektiğini unutmamak önemli.
Yarıçap ve Yükseklik Birimi
Aynı birim kullanmak, sonuçların doğru ve tutarlı olması açısından kritik. Yani, yarıçapı santimetre cinsinden alıyorsanız, yüksekliği de santimetre cinsinden almalısınız. Bu, hesaplamalarınızın doğruluğunu artırır.
Formülü Anlamak
Formülü iyi anlamak, özellikle mühendislik ve mimarlık gibi alanlarda büyük önem taşıyor. Doğru hacim hesaplamaları, yapıların güvenliği ve işlevselliği açısından temel bir rol oynuyor.
Sonuç olarak, silindirin hacmini hesaplarken dikkat edilmesi gereken birçok faktör var. Bu konudaki bilgilendirmelerin, hem öğrencilere hem de meraklılarına faydalı olacaktır. Soruların olursa, yardımcı olmaktan memnuniyet duyarım!
Silindir hacim formülü ile ilgili bilgiler oldukça faydalı. Örneğin, yüsekliği 16 cm ve yarıçapı 8 cm olan bir silindirin hacmini hesaplamak için taban alanını bulup, bu alanı yükseklik ile çarptığınızda sonucu elde ediyorsunuz. Bu formül gerçekten pratik.
Merhaba Soytekin,
Silindir hacim formülü hakkında verdiğin bilgiler gerçekten çok doğru ve faydalı. Silindirin hacmini hesaplamak için taban alanını bulup bu alanı yükseklikle çarpmak, matematiksel olarak oldukça mantıklı ve pratik bir yöntem. Bu hesaplama sırasında kullandığımız formül V = πr²h, burada r yarıçap, h ise yükseklik.
Örneğin, senin belirttiğin gibi, yarıçapı 8 cm ve yüksekliği 16 cm olan bir silindirin hacmini hesaplamak için önce taban alanını (π 8²) buluyoruz ve ardından bu alanı 16 cm ile çarpıyoruz. Sonuç olarak, silindirin hacmini 128π cm³ olarak elde ederiz.
Bu tür pratik formüller, günlük hayatta karşılaşabileceğimiz birçok problem için oldukça yararlıdır. Matematiği daha anlamlı hale getiren örneklerle desteklemen de öğrenim sürecini kolaylaştırıyor. Teşekkürler!
Silindirin hacmini bulma süreci oldukça öğretici. Örneklerde verilen adımlar, formüllerin uygulamasını net bir şekilde gösteriyor. Özellikle yarıçap ve yükseklik birimlerini aynı tutmanın önemi vurgulanmış. Bu, hacim hesaplamalarında doğru sonuçlar elde etmek için kritik bir nokta.
Yorumunuza Teşekkürler
Bengialp, silindirin hacmini bulma sürecinin öğretici olduğunu belirtmeniz çok değerli. Gerçekten de, adım adım ilerlemek ve formüllerin nasıl uygulandığını görmek, konunun daha iyi anlaşılmasına yardımcı oluyor. Özellikle yarıçap ve yükseklik birimlerinin aynı tutulmasının altını çizmeniz, doğru sonuçlar elde etmek için kritik bir nokta. Bu tür ayrıntılar, matematiksel hesaplamalarda sıkça gözden kaçabiliyor. Başka konularda da deneyimlerinizi paylaşmanızı bekliyoruz!
Silindirin hacim formülü hakkında okuduğum bilgiler oldukça faydalıydı. Özellikle kimya hacim formülü ile ilgili örnekler verilmesi, konunun daha iyi anlaşılmasına yardımcı oluyor. Silindirin hacmini hesaplamak için taban alanını ve yüksekliği kullanmak, pratikte çok işe yarıyor. Teşekkürler!
Palmiye,
Silindirin Hacim Formülü ile ilgili düşüncelerinizi paylaştığınız için teşekkür ederim. Bu konunun, özellikle kimya derslerinde hacim hesaplamaları açısından ne kadar önemli olduğunu vurgulamanız oldukça yerinde. Silindirin hacmini hesaplamak için taban alanı ve yükseklik kullanmak, gerçekten de pratik bir yöntem ve birçok uygulamada karşımıza çıkıyor. Örneklerle desteklenmesi, konunun daha anlaşılır hale gelmesine büyük katkı sağlıyor. Eğer daha fazla örnek ve uygulama ile ilgili bilgi almak isterseniz, her zaman yardımcı olmaktan mutluluk duyarım. İyi çalışmalar dilerim!
Gerçekten silindirin hacmini hesaplamak için taban alanı ve yüksekliği kullanmam gerektiğini anlamış bulunuyorum. Fakat pi sayısını 3 yerine 3.14 olarak alsaydım, sonuçlar ne kadar değişirdi?
Merhaba Hüdayi,
Pi sayısını 3 yerine 3.14 olarak almak, hesaplamalarında daha doğru sonuçlar elde etmeni sağlar. Örneğin, taban alanı r^2 pi formülüyle hesaplanır ve yükseklikle çarparak hacmi bulursun. Pi'yi 3 almak, yaklaşık olarak %4.5'lik bir yanlışlığa neden olur. Bu da sonuçlarının gerçekten daha küçük çıkmasına yol açar. Yani, pi'yi 3.14 olarak almak, silindirin hacmini daha doğru ve gerçeğe yakın bir şekilde hesaplamana yardımcı olur.
Sevgiler,
Asistan
- 01 Ekim 2024 Salı
Sabun Formülü Nedir?- 01 Ekim 2024 Salı
10 Sınıf Fizik Formülleri Nelerdir?- 28 Eylül 2024 Cumartesi
Devirli Ondalık Sayılar Formülü- 22 Eylül 2024 Pazar
Eşkenar Üçgen Alan Formülü Nelerdir?- 22 Eylül 2024 Pazar
Tazminat Hesaplama Formülü