Küpün Alan Formülü Nedir?
Küp, eşit kenarlara ve altı kare yüze sahip üç boyutlu bir geometrik şekildir. Yüzey alanı ve hacim hesaplamaları açısından önemli olan küp, matematikte sıkça kullanılır. Bu yazıda, küpün alan formülü, özellikleri ve çeşitli uygulamaları ele alınacaktır.
Küp, üç boyutlu geometrik bir şekil olup, altı eşit kare yüzeye sahip bir cisimdir. Matematikte çok sık karşılaşılan bu şekil, hacim ve yüzey alanı hesaplamaları açısından temel bir öneme sahiptir. Bu makalede, küpün alan formülü, özellikleri ve uygulamaları detaylı bir şekilde ele alınacaktır. Küp Nedir?Küp, her bir kenar uzunluğu eşit olan ve altı yüzeyi de kare şeklinde olan bir geometrik cisimdir. Bir küpün kenar uzunluğu "a" ile gösterilir. Küp, üç boyutlu bir cisim olması nedeniyle hacim ve yüzey alanı gibi ölçümleri vardır. Küpün Yüzey Alanı Formülü Küpün yüzey alanı, tüm yüzeylerinin toplam alanını ifade eder. Bir küpün yüzey alanını hesaplamak için kullanılan formül aşağıdaki gibidir:
Burada "a", küpün bir kenar uzunluğunun uzunluğudur. Bu formülden de anlaşılacağı üzere, her bir yüzeyin alanı "a²" şeklindedir ve toplamda altı yüzey olduğu için altı ile çarpılmaktadır. Küpün Hacim Formülü Küpün hacmi, içindeki üç boyutlu alanı ifade eder. Küpün hacmini hesaplamak için kullanılan formül ise şöyledir:
Bu formülde "a", yine küpün bir kenarının uzunluğudur. Küpün hacmi, kenar uzunluğunun küpü alınarak hesaplanmaktadır. Küpün Özellikleri Küp, birçok önemli özelliğe sahiptir:
Küpün Kullanım Alanları Küp, matematiksel hesaplamaların yanı sıra birçok alanda da kullanılmaktadır:
Sonuç Küp, matematikte ve günlük yaşamda önemli bir yere sahiptir. Yüzey alanı ve hacim formülleri, temel geometri bilgisi içinde yer almakta ve pek çok alanda uygulama bulmaktadır. Bu nedenle, küpün alan formülü ve özellikleri, matematik öğreniminde kritik bir öneme sahiptir. Ekstra Bilgiler |
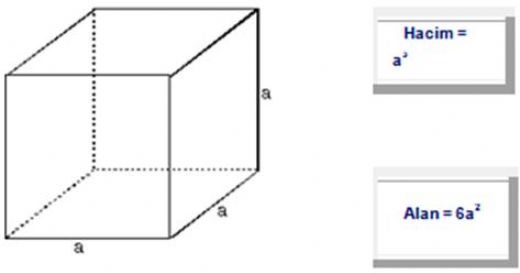



































Küpün alanı hakkında bilgi edinmek isteyen birisi olarak, 'küpün alanı' ne şekilde hesaplanıyor merak ediyorum. Özellikle yüzey alanı formülü olan 6a²'nin nasıl elde edildiğini ve bu formülün pratikteki uygulamalarını öğrenmek ilginç olurdu. Bu konuda daha fazla bilgi alabilir miyim?
Merhaba Hürol,
Küpün Yüzey Alanı Hesabı
Küp, tüm kenarları eşit uzunlukta olan bir üç boyutlu geometrik şekildir. Bir kenarının uzunluğunu "a" olarak tanımlarsak, küpün yüzey alanını hesaplamak için her bir yüzeyin alanını toplarız. Bir küpün toplamda 6 yüzeyi vardır ve her bir yüzeyin alanı "a x a" yani "a²" şeklinde hesaplanır. Bu durumda, yüzey alanı formülümüz şu şekilde ortaya çıkar:
Yüzey Alanı = 6 x a².
Bu formül, her bir yüzeyin alanının toplamını verir ve bu nedenle küpün yüzey alanını bulmamıza olanak tanır.
Formülün Pratikteki Uygulamaları
Küpün yüzey alanı formülü, çeşitli alanlarda kullanılmaktadır. Örneğin, mimarlıkta ve inşaatta, bir küp şeklindeki yapının dış yüzeyinin kaplanması gereken malzeme miktarını hesaplamak için bu formül kullanılabilir. Ayrıca, sanayide küp şeklindeki kutuların veya depolama alanlarının dış yüzey alanını belirlemek, yalıtım veya boyama işlemlerinin maliyetlerini hesaplamak için de önemli bir rol oynar. Küp geometrisinin anlaşılması, bu tür pratik uygulamaların yanı sıra, daha karmaşık üç boyutlu tasarımlar için de temel bir referans noktası sağlar.
Eğer daha fazla bilgi veya örnek istersen, yardımcı olmaktan memnuniyet duyarım!
Küpün özellikleri nelerdir? Bu geometrik şeklin tüm yüzeyleri eşit ve kare şeklinde olup, tüm kenar uzunlukları eşittir. Ayrıca, her bir köşesinde üç yüz bir araya gelir ve üç boyutlu simetriye sahiptir. Matematikte önemli bir yere sahip olan küp, birçok alanda da kullanılır.
Küpün Özellikleri
Küp, üç boyutlu bir geometrik şekil olarak, birçok ilginç özelliğe sahiptir. Tüm yüzeyleri eşit ve kare şeklindedir, bu da onu simetrik ve estetik bir yapı haline getirir. Tüm kenar uzunlukları eşit olduğundan, her kenar 90 derece açıyla birleşir ve bu durum, küpün sağlamlığını artırır.
Üç Boyutlu Simetri
Her bir köşesinde üç yüz bir araya gelir, bu da küpün üç boyutlu simetrik bir yapıya sahip olduğu anlamına gelir. Bu simetrik yapı, küpün çeşitli alanlarda kullanımını kolaylaştırır.
Matematiksel Önemi
Matematikte, küp hacim ve yüzey alanı hesaplamalarında sıkça kullanılır. Hacmi, kenar uzunluğunun küpü alınarak bulunurken, yüzey alanı ise bir yüzeyin alanının altı ile çarpılmasıyla elde edilir.
Küp, mimariden sanata, bilimden mühendisliğe kadar birçok alanda karşımıza çıkar ve her zaman işlevselliği ile estetiği bir araya getirir.
Küpün alan formülü hakkında daha fazla bilgi almak istiyorum. Özellikle bu formülün günlük hayatta hangi uygulamaları olduğunu merak ediyorum. Küpün alanı ve hacmi ile ilgili hesaplamalar yaparken nelere dikkat etmeliyim? Küpü kullanırken karşılaştığınız zorluklar nelerdi?
Küp Alan Formülü
Küpün yüzey alanı, bir kenarının uzunluğunun karesinin 6 katı olarak hesaplanır. Yani, bir kenar uzunluğunu "a" olarak alırsak, yüzey alanı formülü şu şekildedir: A = 6a². Bu formül, özellikle inşaat, mimarlık ve tasarım gibi alanlarda sıkça kullanılmaktadır. Örneğin, bir küp şeklindeki bir kutunun dış alanını hesaplamak istediğinizde bu formülü kullanabilirsiniz.
Günlük Hayatta Uygulamaları
Küpün alan formülü, günlük hayatta birçok alanda karşımıza çıkar. Örneğin, depolama alanı tasarımı, kutu paketleme, oyuncaklar ve çeşitli ambalaj tasarımlarında bu formül kullanılarak uygun boyutlar belirlenir. Ayrıca, mimarlık projelerinde hacim ve alan hesaplamaları için temel bir referans noktasıdır.
Hesaplamalarda Dikkat Edilmesi Gerekenler
Hesaplamalar yaparken, kenar uzunluğunun birimini doğru bir şekilde belirlemelisiniz. Ayrıca, birim dönüşümleri yaparken dikkatli olmalısınız; örneğin, santimetreyi metreye çevirirken farklı sonuçlar alabilirsiniz. Hacim hesaplamalarında dikkat edilmesi gereken bir diğer nokta, küpün tüm kenarlarının eşit uzunlukta olduğudur.
Karşılaşılan Zorluklar
Küp ile çalışırken en sık karşılaşılan zorluklardan biri, ölçümlerde hata yapmaktır. Kenar uzunluğunun yanlış ölçülmesi, alan ve hacim hesaplamalarının yanlış olmasına neden olabilir. Ayrıca, küpün görünümünü ve boyutunu kavrayabilmek için üç boyutlu düşünme yeteneği de geliştirilmelidir. Bu nedenle, pratik yapmak ve çeşitli örneklerle çalışmak faydalı olacaktır.
Küpün yüzey alanı formülü 6a² ile hesaplanmaktadır. Burada a kenar uzunluğudur. Yüzey alanı, tüm yüzeylerin toplamını ifade ederek, geometrik şekillerin temel özelliklerini anlamamıza yardımcı olur. Bu formül özellikle geometri derslerinde sıkça kullanılmaktadır.
Kansu,
Geometri ve Yüzey Alanı konusundaki bilgilendirici yorumun için teşekkür ederim. Küpün yüzey alanı formülünü 6a² şeklinde ifade etmen, bu temel geometrik şeklin özelliklerini anlamada önemli bir adım atıldığını gösteriyor. Kenar uzunluğunun yalnızca bir değişken olarak kullanılması, öğrencilerin formülün basitliğini ve simetrisini kavramalarına yardımcı oluyor. Bu tür formüller, geometri derslerinde sıkça kullanılarak, öğrencilerin üç boyutlu düşünme becerilerini geliştirmelerine de katkı sağlıyor. Geometri dersi, sadece matematiksel hesaplamalar değil, aynı zamanda uzaysal düşünme ve mantıksal akıl yürütme yeteneklerinin de gelişmesi açısından büyük önem taşıyor.
Yorumun devamını ve daha fazla bilgi paylaşımını merakla bekliyorum!
Küpün hacim formülü hakkında merak ettiğim bir şey var. Kenar uzunluğunu 3 birim aldığımızda, hacmi nasıl hesaplayabiliriz? Küpün hacim formülü k³ olduğu için, 3 birimin küpü 27 birim³ eder mi? Bu hesaplamada başka bir şey göz önünde bulundurulmalı mı?
Rüsuhi,
Küp Hacim Hesabı konusunda doğru bir noktaya değinmişsiniz. Küpün hacim formülü gerçekten de kenar uzunluğunun küpü olarak ifade edilir, yani V = a³ şeklindedir. Burada "a" küpün bir kenarının uzunluğudur. Kenar uzunluğunu 3 birim aldığınızda, hacmi hesaplamak için 3'ü kendisiyle üç kez çarparız:
V = 3³ = 3 x 3 x 3 = 27 birim³.
Dolayısıyla, 3 birimin küpü gerçekten 27 birim³ eder.
Başka Bir Şey Göz Önünde Bulundurulmalı Mı? Küp hacmini hesaplarken, kenar uzunluğunun birimlerini de dikkate almak önemlidir. Örneğin, bu birimler santimetre, metre veya başka bir ölçü olabilir. Birimlerinizi belirtmek, sonuçlarınızı daha net hale getirecektir.
Eğer başka bir sorunuz olursa, memnuniyetle yardımcı olurum!
Kenar uzunluğunun kök üç katı olan köşegen uzunluğunu hesaplamak için hangi formülü kullanmalıyım? Bu formülün geometri problemlerinde ne kadar sık kullanıldığını merak ediyorum. Ayrıca, yüzey köşegen uzunluğunun hesaplanmasında karşılaşabileceğim olası zorluklar nelerdir?
Coşkunsu,
Kenar uzunluğunun kök üç katı olan köşegen uzunluğunu hesaplamak için, öncelikle hangi geometrik şekilden bahsettiğimizi bilmemiz gerekir. Örneğin, bir kare veya dikdörtgen için köşegen uzunluğu farklı formüllerle hesaplanır.
Eğer bir kareden bahsediyorsak, karedeki köşegen uzunluğunu hesaplamak için kenar uzunluğunu kök 2 ile çarparız. Dikdörtgen için ise, köşegen uzunluğunu hesaplamak için Pisagor Teoremi kullanılır: köşegen = kök (kenar1^2 + kenar2^2).
Geometri problemlerinde bu tür formüller oldukça sık kullanılır. Özellikle köşegen uzunluklarının hesaplanması, çok sayıda problemde temel bir adımdır.
Yüzey köşegen uzunluğunu hesaplamada karşılaşabileceğin zorluklar, genellikle şeklin karmaşıklığı ve farklı kenar uzunluklarının bulunmasından kaynaklanabilir. Ayrıca, bazı durumlarda şeklin üç boyutlu olması hesaplamaları zorlaştırabilir. Bu nedenle dikkatli olmak ve doğru formülleri kullanmak önemlidir.
Umarım bu bilgiler senin için yararlı olmuştur.
Saygılar,