
Trigonometri Formülleri Nelerdir?
Trigonometri, üçgenlerin açıları ve kenarları arasındaki ilişkileri inceleyen bir matematik dalıdır. Bu yazıda, temel trigonometri kavramları, önemli formüller ve çeşitli uygulama alanları hakkında bilgi verilmektedir. Trigonometri, mühendislikten mimarlığa kadar birçok alanda kritik öneme sahiptir.
Trigonometri, üçgenlerin açıları ve kenarları arasındaki ilişkileri inceleyen matematik dalıdır. Özellikle dik üçgenlerde uygulanan temel kavramlar ve formüller, mühendislik, fizik ve mimarlık gibi birçok alanda önemli bir yere sahiptir. Bu makalede, trigonometri formüllerine dair kapsamlı bir inceleme sunulacaktır. Trigonometri Temel Kavramları Trigonometri, üçgenlerin özelliklerini anlamak için bazı temel kavramlar içerir. Bu kavramların başlıcaları şunlardır:
Trigonometri Formülleri Trigonometri, birçok formülle desteklenmektedir. Aşağıda, en yaygın kullanılan trigonometri formüllerine dair bir liste sunulmuştur:
Trigonometri Uygulamaları Trigonometri, birçok alanda uygulama bulmaktadır. Bu uygulamalardan bazıları şunlardır:
Ekstra Bilgiler Trigonometri, sadece dik üçgenlerle sınırlı değildir. Aynı zamanda dairesel trigonometri olarak adlandırılan bir alan da bulunmaktadır. Dairesel trigonometri, bir çember üzerindeki açıların ve kenarların ilişkilerini inceler. Ayrıca, trigonometri hesaplamaları için çeşitli hesap makineleri ve yazılımlar mevcuttur. Bu araçlar, karmaşık hesaplamaları hızlandırmakta ve daha doğru sonuçlar elde edilmesine yardımcı olmaktadır. Sonuç olarak, trigonometri formülleri, matematiğin temel taşlarından birini oluşturarak birçok alanda uygulama bulmaktadır. Bu formüllerin doğru bir şekilde anlaşılması ve uygulanması, bilimsel ve mühendislik çalışmalarında büyük bir avantaj sağlamaktadır. |
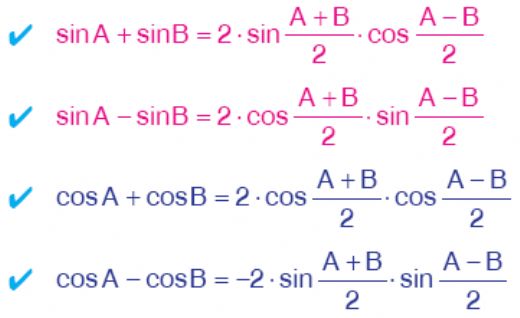















































Trigonometri ile ilgili bu bilgiler çok faydalı. Özellikle üçgenlerin açıları ve kenar uzunlukları arasındaki ilişkiyi anlamak için temel kavramların bilinmesi gerektiğini belirtmen çok önemli. Açılara göre sinüs, kosinüs, tanjant ve kotanjant oranlarının nasıl hesaplandığını öğrenmek de oldukça yararlı. 30°-60°-90° ve 45°-45°-90° özel üçgenlerinin trigonometrik oranlarını bilmek, matematik problemlerini çözerken büyük bir avantaj sağlar. Bu formülleri kullanarak daha karmaşık trigonometrik eşitlikler oluşturmak ve dönüştürmek de oldukça eğlenceli. Tüm bu bilgileri öğrenmek, günlük hayatta ve mühendislik gibi alanlarda karşılaşabileceğimiz trigonometrik problemleri çözmek için kesinlikle gerekli. Peki, bu formülleri uygularken en çok zorlandığın kısımlar neler?
Merhaba Şahsüvar,
Yorumunuzda trigonometri ile ilgili önemli noktalara değindiğiniz için teşekkür ederim. Trigonometri, gerçekten de günlük yaşamda ve mühendislikte sıkça karşımıza çıkan bir alan. Üçgenlerin açıları ve kenar uzunlukları arasındaki ilişkileri anlamak, birçok matematiksel problemi çözmede büyük bir temel oluşturuyor.
Temel Kavramların Önemi
Trigonometri oranları olan sinüs, kosinüs, tanjant ve kotanjantın hesaplanması, bu alanın anlaşılması için kritik öneme sahip. Özellikle özel üçgenlerin trigonometrik oranlarını öğrenmek, birçok problemi daha hızlı çözmemizi sağlıyor.
Zorlandığınız Kısımlar
Formülleri uygularken zorluk yaşadığınız kısımlar genellikle karmaşık eşitliklerin çözümü veya farklı trigonometrik kimliklerin bir arada kullanılması olabilir. Bu süreçte, formüllerin mantığını kavramak önemli. Ayrıca, trigonometrik dönüşümler ve açıların birbiriyle ilişkisi konusunda da sıkıntılar yaşanabiliyor.
Bu tür zorluklar, pratik yaparak ve farklı problem türleri üzerinde çalışarak aşılabilir. Umarım bu bilgiler sizin için faydalı olmuştur. İlgili olduğunuz başka bir konu varsa, yardımcı olmaktan memnuniyet duyarım.